Haar測度の構成

この記事は好きな証明AdventCalender 2018の10日目です。

adventar.org

　次の定理があります。

（局所）コンパクト位相群の左（右）移動で不変な測度（Haar測度）は存在します。

　この証明の、おおざっば（）な筋書きを、二通り紹介します。 この２つはほとんど同じことをやっており、まったく同じ飛び道具を使って測度をﾊﾞﾊﾞｰﾝと作ってしまいます。 このﾊﾞﾊﾞｰﾝ部分が無駄にCool（と僕は思った）なので、それをシェアしたいというものです。

１.まずそれは何

　Haar測度が何で、それがあるとなぜうれしいかという話をします。 測度というのは（部分）集合の大きさを測るものです。 集合には論理演算ができて、特に排他的和があります。 集合から正実数の割当てでこの排他的和を和にうつす（可算個でもOKなもの）を測度といいます。 測度の定義域は、ある集合族で、集合の（可算個の）和積補集合で閉じるものです。これを可算加法族といいます。

\Sigma\subset 2^\mathbb{\Omega}

\mu:\Sigma\rightarrow \mathbb{R}

\mu (\sum_i X_i)=\sum_i\mu(X_i) (X_i\cap X_j = \emptyset (i\neq j))

測度論 - Wikipedia

　測度があると、積分ができ、これをルベーグ積分といって、 大抵の場合リーマン積分よりも（収束性や連続性といった）性能が良いです。

　位相群というのは位相情報をもった群で、例えば身近なものでは回転群、並進群、あるいはこの組み合わせ、 物理の人なら、ポアンカレ群、ゲージ群などもそうです。群の演算が全部それがもつ位相について連続なものです。 局所コンパクト＝「コンパクトな近傍がある」が条件についていますが、 応用系の人がすぐ思いつく連続位相群はだいたいそうなのであまり気にしなくてよいです。

位相群 - Wikipedia

　位相群上の測度が左不変であるとは、群の可測集合(測度で測れる集合)に対する左作用で、測度の値が変わらないことを指します。 つまり、\mu(gX)=\mu(X)です。gX=\{gx|x\in X\}と略記します。 別に右でもよいのですが、Haar測度と言ったときは慣習上左のことが多いです。

　さて、なぜこれがあると良いのでしょうか？　一つには、（めっちゃ一般化された）フーリエ解析をやりたいのです。 ご存知フーリエ解析は、\exp(ikx)で\mathbb{R}上の関数を展開してﾜｰｰｰッとやります。 ここで「\mathbb{R}は可換な局所コンパクト位相群で、\exp(ikx)はその既約表現である」という事実があります。 じつはこれは一般の位相群に拡張できるのです。つまり一般に位相群の上の関数の情報を、その群の表現の成分で解析できるのです。 そのとき、群上の関数を積分したくなります。すると測度がほしいですが、どんなものが良いでしょうか？ 群作用があるので、これに素直に振る舞ってくれるものがよいです。まさにそこにHaar測度が使えるのです。 というわけで、Haar測度は群上の関数解析になくてはならないものです。

２.証明の筋書き：前編

　では、このHaar測度はどうやって作ればいいでしょうか？　実は具体的なリー群とかであれば、 具体的にエイヤッと計算できることが多いです。実際それで間に合ってしまいます。 ところが、特にそういった具体的な情報がなくても、存在は保証されてしまいます。これが今回の定理です。 存在する、ということは（構成的じゃないかもしれないけど）なんらかの測度のつくり方があるわけですが、 一体どうやるんでしょうか？

ここで、文献情報です。この記事は次の２本の証明をベースにします。

[1]https://www.math.uchicago.edu/~may/VIGRE/VIGRE2010/REUPapers/Gleason.pdf

[2]G.B.Folland A course of abstract harmonic analysis

https://www.amazon.co.jp/Abstract-Harmonic-Analysis-Textbooks-Mathematics/dp/1498727131

　証明を眺める前に、この２つの証明はある意味でほとんど同じことをやっているのですが、 これがどういった意味で同じであるかというのを補足します。

まず測度を作る必要があるのですが、局所コンパクトハウスドルフ空間（位相群もハウスドルフです）上の ラドン（位相に対して適当に性質が良い）測度と、その上の連続関数環の双対空間が１対１対応するという事実が知られています。 これはRiesz-Markov-Kakutaniの定理と呼ばれています。

リースの表現定理 - Wikipedia

　どういうことでしょうか？めちゃくちゃざっくり言うと、「積分と測度はおんなじ」という主張です。 測度があると、積分ができます。積分とはどんな写像でしょうか？それは、その空間の関数を、線形にスカラーに移します。 関数がある程度小さいか、測度がある程度小さいならば、この写像は有界になるでしょう。 つまり、測度から、関数空間からの線形汎関数、つまり関数空間の双対空間の元を手に入れられます。 そしてその逆が成り立つ、というのがRMKの主張です。関数空間の双対空間から、測度が手に入ります。

この意味で、測度を議論することと、積分に相当する汎関数を議論することは等価です。 先の２文献の違いは、[1]は前者の、[2]は後者の立場で構成をやっているという点です。それ以外の部分は概ね似通っています。 測度の場合の左不変性は\mu(xX)=\mu(X)ですが、これを積分に翻案すると、 群上関数の左移動を

(L_g f)(x)=f(g^{-1}x)

で、定めると、

\int L_g f(x) d\mu(x)=\int f(g^{-1}x) d\mu(x) = \int f(x) d\mu(gx)= \int f(x) d\mu(x)

なので、左不変な測度を見つけるかわりに、群上関数環の線形汎関数FでFL_g=Fであるようなものを見つけても良いです。

まず[1]の構成を眺めてみましょう。 コンパクト集合Vを一つとって、他のコンパクト集合Kに対して(K;V)なる量を次のように定義します。

(K;V)=\inf \{\#I |K\subset \cup_{i\in I} g_iV\}

これはどういう量でしょうか？今群構造を使うことで、Vをいろんな位置に動かすことができます。 Vを左移動させて、これをいくつかつかってKを被覆します。

直感的には次のような感じです。

f:id:phykm:20181211011623j:plain
KをV３つで被覆

図が汚い…お絵かき能力のNASA…

Vが内部を持っていれば、Kのコンパクト性からこれは有限個で済みます。この最小の数が(K;V)です。 つまり、直感的には「KがV何個分か？」という量です。測度っぽいですね。 実際測度っぽい性質がいくつか成り立ちます。

単調性

K_1 \subset K_2 \Rightarrow (K_1;V)\le (K_2;V)

劣加法性

(K_1\cup K_2 ; V)\le (K_1;V)+(K_2;V)

連鎖律

(K_1;K_3)\le(K_1;K_2)(K_2;K_3)

そして大事ですが左不変性も成り立ちます。Vの移動に左移動を使っているからです。

しかしこの「測度」はVを１単位としているので、めちゃくちゃ粗いです。実際加法性ではなくて、劣加法性です。 ではVをどんどん小さい集合にとっていけばいいかというと、今度は(K;V)の値がどんどん大きくなってしまいます。 そこで、これを相対化した次を考えます。もう一つコンパクト集合K_0を固定して

I_V(K)=(K;V)/(K_0;V)

と定義します。こうしても以上の測度っぽい性質は全部継承されます。 しかも、今度はVを小さくして行けば、分母と分子両方が大きくなって行くので、 I_Vの値自体は大きくならず、どんどん精度がよくなっていきます。 しかし、

V = \emptyset だとか、

V = \{ e \} とは置けません。

なんらかの極限を取る必要があります。 その極限はどうやって作ったら良いでしょうか？

ここのネタバラシは次節にして、[2]の構成も見てみましょう。やっていることはとても似ています。 こんどは線形汎関数を作るので、コンパクト集合ではなく、コンパクトサポートな正値関数vを一つ固定します。 これを使って、他のコンパクトサポート正値関数fに対して(f;v)なる量を次のように定義します。

(f;v) = \inf \{ \sum _i c_i | f \le \sum_i c_i L_{g_i} v, c_i > 0 \}

考え方は一緒で、関数であるために値が連続的になりますが、これも「fはvいくつ分か？」という量です。 まったく同様に、単調性、劣加法性、連鎖律、左不変性が成り立ち、加えて定数倍をそのまま通します。

(cf;v)=c(f;v)

やはりvをどんどん「小さく」、具体的にはvのサポートを小さくすることで、この精度を上げたいのですが、 このままではどんどん大きくなってしまうので、これも相対化します。もう一つコンパクトサポート正値関数f_0を固定して

I_v(f)=(f;v)/(f_0;v)

を定義します。そしてvのサポートをどんどん小さくしていきます。ここでも同様に極限を取る必要があります。

３．証明の筋書き:後編

　では以上のI_V,I_vの「Vを小さくする極限」をどうとったらいいでしょうか？ この極限は、「同じ場所」で取りたいので、群単位元の近傍系とします。

ここで道具を２つ用意します。

　ある閉集合族が有限交差性をもつ、とは、それらの有限個の積が空でないことを言います。 Xをコンパクトな空間として、有限交差性を持つその部分閉集合属をFとしましょう。 このとき、\cap F\neq \emptysetであることが次のように示せます。

背理法を使います。\cap F=\emptysetであるとします。このとき\cup_{A\in F}A^c=Xです。 A^cは開集合なので、これは開被覆であり、コンパクト性から、有限個のA_1\dots A_nをとって \cup_{i=1}^n A_i^c=Xとできます。したがって、\cap_{i=1}^n A_i=\emptysetとなりますが、 これは有限交差性に反します。よって、\cap F\neq \emptysetです。

それから、チコノフの定理というものも用意します。これは次のような定理です。

コンパクト空間の直積空間は（何個の積でも！）直積位相でコンパクトである。

チコノフの定理 - Wikipedia

さて、I_V,I_vの極限を取りましょう。実はコンパクト集合K、及びコンパクトサポート関数fを固定すれば、 I_V(K),I_v(f)のとる値は、V,vによらない有界閉区間に収まることが示せます。これをX_K,X_fとしましょう。

\mathcal{K}をコンパクト集合全体、C_c^+(G)をコンパクトサポート正値関数全体とします。 これを用いて、

\Pi_{K\in \mathcal{K}} X_K

\Pi_{f\in C_c^+(G)} X_f

というめっちゃでっかい直積位相空間を作ります。 これは、今ほしいものが集合族から正実数、ないし関数空間から正実数の関数なので、 それを性質によらずぜーーーんぶ含んでしまう巨大な空間をまず作ってしまおうというものです。 実数の有界閉区間はコンパクトですから、チコノフの定理から、この巨大な空間も、巨大なのにコンパクトです。

そして、単位元近傍N\in\mathcal{N}ごとに、粗い測度の集合を

\mu(N)=\{I_V| V \in \mathcal{K},V\subset N \}\subset \Pi_{K\in \mathcal{K}} X_K

M(N)=\{I_v| v \in C_c^+(G), \mathrm{supp} v \subset N \}\subset \Pi_{f\in C_c^+(G)} X_f

と、このでっかい空間の部分集合とみなしてしまいます。 \mu(N)は、左不変な「粗い測度」で、分解能がNよりもいいもの全体、 M(N)は、左不変な「粗い線形汎関数」で、分解能がNよりもいいもの全体、 と読むことができます。

そして、極限をとるかわりに、これの直積位相で閉包\overline{\mu(N)},\overline{M(N)}をとります。 閉包と簡単にいいましたが、実質的にその空間の収束列の収束先をすべて含めることなので、 ここで極限をとっていることになります。 つまり、\overline{\mu(N)},\overline{M(N)}には、めっちゃ精度のいい測度/線形汎関数が含まれているはずです。 しかしその精度のよいものをどうやって取り出せばいいでしょうか？ このままでは精度の悪いものも一緒に含まれているので、どれを取ればいいのかわかりません。

ここで実は

\cap_{i=1}^n \overline{\mu(N_i)}=\overline{\mu(\cap_{i=1}^n N_i)}

\cap_{i=1}^n \overline{M(N_i)}=\overline{M(\cap_{i=1}^n N_i)}

が成り立ちます。N_iは、単位元の近傍をとることとしました。近傍系は有限交差性をもちました。 このことから\{\overline{\mu(N)}\}_{N\in\mathcal{N}},\{\overline{M(N)} \}_{N\in\mathcal{N}}も有限交差性を持ちます。 なぜなら、近傍の有限個の交差は再び近傍であり、\overline{\mu(-)},\overline{M(-)}は任意の近傍について空でないからです。

すると、直積空間のコンパクト性と、有限交差性から

\cap_{N\in \mathcal{N}} \overline{\mu(N)}

\cap_{N\in \mathcal{N}} \overline{M(N)}

が「空でない」ことがわかります。この要素はあらゆるN\in \mathcal{N}よりも細かい分解能を持つ、 めちゃくちゃ精度のよい測度/線形汎関数です。実際、以上の議論をもっときちんとやると、 ここに含まれる要素にはちゃんと加法性\mu(\sum_i X_i)=\sum_i \mu(X_i)が成り立ちます。 つまり、我々の望む測度/汎関数が手に入りました。あとはこれらの定義域を自然に拡張することで、Haar測度が手に入ります。

４．何が面白いのか

　僕は学部で一般位相をやった当初、チコノフ定理のどこがすごいのかまったくわかりませんでした。 しかし解析学をもうちょっと踏み込んでみると、以上のように、コンパクト性がほしいときにすごいパワーを発揮したりします。 コンパクト集合の直積がコンパクト、というとなんでもないようですが、 この直積の数はどれだけ大きくてもよいのです。すごいですね。

　また、以上の作り方は、ほしい要素の素材を、あるデッカイ空間に埋め込んで、そこで極限をとってくる、というやり方をしています。 これってとってもスマートだと思いませんか？　例えばシュワルツの超関数とかも、ある意味では同じようなことをしています。 デルタ関数はある関数の極限として定義されますが、普通の関数空間でやっても特異性がでてきてダメです。 しかし、テスト関数の双対空間でなら、その極限が意味を持ちます。

　あと単純に、I_V,I_vのつくり方がかっこいい。

　以上Haar測度の作り方でした。きちんとした証明が気になる人は、元文献を読んでみてください（そして教えて）

めしレポ

　長きに渡り飯に謎の緊縮政策（意識だけ）をとっていたが、

近年「普通に面白いものを食べて食UXを上げたほうがコスパいいのでは？？？？？？？？？？？？」と転換し、

異次元緩和を発動、学生身分を駆使して昼に飯に乗り出すようになったため、以下レポっす。

　なお飯選びの基準ポイントとして、 「国名・地域名を標榜できるもの」「（可能なら）ランチ営業をしているもの」 を採用しています。これは何故かと言うと、

  • 地域から日本周辺を外すことでUXが上げられる。

  • 流行を考慮しないので混雑を避けられる。行列や予約が不要。

  • ランチは回転率を上げて薄利多売にする傾向があるのでディナーより割安で食べられる。

　検索方法は (国名・地域名) ランチ とかでググるのが最適ですが、 次のようなサイトもあります。

e-food.jp

　見返してみると何故かいまんとこユーラシア周辺から出ていない。

ベトナム：サイゴンフォー（新大塚）

本場ベトナムの味 サイゴン フォー Saigon Pho
本場ベトナムの味 サイゴン フォー Saigon Pho
〒170-0005 東京都豊島区南大塚2-15-6 金文字ビルB1F
03-3946-4701
地図や店舗情報を見る
Powered by ぐるなび

ビル地下にある。名前の通りフォー。サイドメニュー（生春巻きとか）とのセットがあった。 麺のボリュームがある。アクセス良好。

ベトナム：・チョップスティックス（高円寺）

チョップスティックス 高円寺店
チョップスティックス 高円寺店
〒166-0002 東京都杉並区高円寺北3-22-8 大一市場
3,000円（平均）1,000円（ランチ平均）
03-3330-3992
地図や店舗情報を見る
Powered by ぐるなび

ここもサイドメニューとのセットがある。↑よりパクチーが効いている印象。 飲食店街の一角で、他にも変な店がある。

シンガポール：海南鶏飯（水道橋）

シンガポール 海南鶏飯 水道橋本店
シンガポール 海南鶏飯 水道橋本店
〒101-0061 東京都千代田区三崎町2-1-1
2,500円（平均）950円（ランチ平均）
03-3264-7218
地図や店舗情報を見る
Powered by ぐるなび

チキンライスはつけダレの味が濃いめではっきりしている。揚げ版のチキンライスがあるので、 食事としての充足度はある。土日はランチ関係なく日中同一やっているのでアクセスが楽。 夜一人で言ってチキンライスシュッと食って帰るなども可能。

マレーシア：クアラルンプール（本郷）

クアラルンプール - 本郷三丁目/東南アジア料理（その他） [食べログ]

チキンライスは↑よりもタレの味は弱め。パクテーはスープが黒く漢方の味がして面白い。 スープが黒いのがマレー流、スープが透明なのがシンガポール流らしい。

タイ：ゲウチャイ（新宿）

タイ国料理 ゲウチャイ 新宿店

食べログ タイ国料理 ゲウチャイ 新宿店

トムヤムクンを食べた。スープはマイルドでインパクトはそんなにない。 立地がよくてメニューも豊富なので使い勝手はいいかも（一人で夜行っても問題なし）

タイ：ソムオー(新大久保)

ソムオー 新大久保店

食べログ ソムオー 新大久保店

ランチを食べた。安くてメニュー豊富な印象。ランチについてるトムヤムスープは↑よりも刺激が強い。

タイ：タイダイニング（早稲田）

タイ居酒屋 藤田 （【旧店名】タイダイニング） - 早稲田/タイ料理 [食べログ]

ガパオライス的なセット食べた。学生街だからか値段の割にボリュームがすごい。

中華（蘭州ラーメン）：火焔山（池袋）

蘭州拉麺店 火焔山 （ランシュウラーメン カエンザン） - 池袋/中華料理 [食べログ]

シシカバブ的な肉を一本から注文できるので気軽にタンパク質を補給できる。麺はちょっと後半飽きるかも。 蘭州麺は牛だしとパクチーの芳香を味わう食べ物ということでいいですか？

中華（蘭州ラーメン）：馬子禄（神保町）

馬子禄 牛肉面

食べログ 馬子禄 牛肉面

蘭州ラーメンのみ。↑より完成度は高いと思う。初回時ラー油が入りすぎてて味がわからなくなってたので、 ラー油別皿にしてくれるように頼み、まず素でスープを飲むのを推奨。 もとのスープの油分が少ないのでラー油の効きが強い。

ロシア：海燕（春日）

海燕 （カイエン） - 春日/ロシア料理 [食べログ]

ビーフストロガノフは酸味があってやや軽め。洋食ナイズされている気もする。 ロシアンティーのジャムがちゃんと別皿で出てくる。店内は狭いが綺麗で居心地が良い。 ピロシキも食べられる。

ロシア：ろしあ亭（神保町）

ろしあ亭 （ロシアテイ） - 神保町/ロシア料理 [食べログ]

ボルシチとつぼ焼きクリームはここが自分の中のスタンダード。うまい。 ボルシチは甘く（トマトが主張しすぎてない）、つぼ焼きは濃厚（カロリー濃度高そう）。 ディナーも一度行ったが前菜がうまくてよかった。 繁忙期にLOギリギリに行くと入れないことがあるので注意。

ロシア：サラファン（神保町）

サラファン

食べログ サラファン

丁寧な接客、というより店が地階で狭いので客の動線をコントロールしないと厳しい。 つぼ焼きを食べたが、チキンが多く入っていてクリームが負けており、個人的にはろしあ亭のほうが好み。

ロシア：スンガリー（新宿三丁目）

スンガリー 新宿三丁目店

食べログ スンガリー 新宿三丁目店

格調高め。値段も高め。何食ったか忘れた…確かつぼ焼き。 ロシアンティーのジャムが多種類出てきて面白い。 場所が超絶わかりにくい。ディナー用の別店舗があるらしい。

ロシア：チャイカ（高田馬場）

チャイカ

食べログ チャイカ

ビーツが後乗せで入っているものの、ボルシチがほぼトマトベースになっている。 ただし濃厚なので食事としては充足度高い。ランチ営業長め＋アクセス良好。 メインが何かしらのソテーだったりで洋食ナイズされているが、普通の食事としてはおすすめ。

ロシア(グルジア)：カフェロシア(吉祥寺)

Cafe RUSSIA 吉祥寺

食べログ Cafe RUSSIA 吉祥寺

カフェ飯と油断していたところ大皿になみなみと注がれたボルシチがでてきた。 ビーツがガッツリ入っていてきちんと赤い。ちょっと肉の出汁が弱いかも。 つぼ焼きクリームもちゃんとクリームしていた。 「毛皮のコートを着たニシン」（ハッシュドポテトとビーツの間にニシン漬けを敷いたもの）も食える。 なにげにランチ営業がかなり長い。都心からやや遠いが穴場。

クルディスタン：メソポタミア（十条）

クルド家庭料理 手芸カフェ メソポタミア - 十条/西アジア料理（その他） [食べログ]

地域一帯定番のシシカバブは大型の焼き鳥っぽい味。味もちょうどいい。 羊飼いサラダ（生野菜と角切りトマトを和えた奴）は他店の相当品よりも食べやすく感じた。 唐辛子、ラー油を多用しているように見えるが、種は除いてあるのかそれほど辛くはない。 ヨーグルトとナスを和えた不思議な冷製スープ（ほぼ半固形）があり、不思議な味。

ブルガリア：トロヤン（銀座）

ブルガリアンダイニング トロヤン 銀座

食べログ ブルガリアンダイニング トロヤン 銀座

ランチビュッフェ。ヨーグルトが多用されている。↑とはまた違うヨーグルトスープ（こんどはちゃんと液体）がある。 羊飼いサラダに似たトマト角切り生野菜サラダがあるが、チーズがかかっている。乳製品プッシュ。 ヨーグルトとチーズの中間みたいなやつがポテサラの地位にある。ムサカなるひき肉オーブンを食べたが、 肉の味がトルコのイスケンデルに似ている。で、やはりヨーグルトソースがかかっている。 メゼはなかった。コスパは良い。

トルコ：ヒサル（大久保）

トルコ料理レストラン ヒサル

食べログ トルコ料理レストラン ヒサル

ランチと夕食一回ずつ。駅からアクセスもよく、コスパもいい。 フムスもある。白濁するアニス酒のラクも飲める。メゼは食べてない。 イスケンデルはちょっと味がくどいかも。

トルコ：ボスボラスハサン（新宿二丁目）

ボスボラス ハサン 新宿二丁目店 （BOSPHORUS HASAN） - 新宿三丁目/トルコ料理 [食べログ]

夕食。↑よりもちょっと格調高い雰囲気。でも高くはない。 ラム肉がうまかった。肉料理の肉の味付けが結構濃い気がする。ラクもある。 塩味のアイラン（飲む塩ヨーグルト）があり、確かに味の濃い料理と合う。塩分過多なりそう。 メゼ・ペースト系も満足できる味とボリューム。 トルコ料理いろんなメゼをパンでいじりながら酒を飲んでればだいたい完成しそう（偏見）。

イラン：アラジン（六本木）

アラジン - 六本木/西アジア料理（その他） [食べログ]

ランチビュッフェをやっているのでたくさん食べられるが、なかなか料理の癖が強い。 行ったときは日本人がほとんど居なかった。

シリア：ゼノビア（広尾）

アラビアレストラン　ゼノビア

食べログ アラビアレストラン　ゼノビア

ランチを食べた。前菜のサラダだけはちょっと味がキツく、好き嫌いが分かれそう。 それ以外はだいたい食べやすくボリュームもある。 個人的にランチプレートについてるオリーブと野菜の和え物がうまくてすき。 限定10食と書いてあるがランチ終了ギリギリに行っても割とまだ頼めたりした。 店内が凝ってて趣がある。高UX。

スウェーデン：リラ・ダーラナ（六本木）

北欧料理リラ・ダーラナ

洋食と違う味付けが面白い。ボリュームもそこそこあって安くて美味しい。田舎っぽい味。 ピクルスの酸味がところどころ感じられてメインの味を中和している。

チェコ：セドミクラースキー(代々木上原）

Sedmikrasky（セドミクラースキー）

これも洋食とは違う味付け。メニューは少ないが、メイン皿料理が安心する味で完成度高い。 ローストポークとザワークラウトと茹でパンのディッシュがすき。完璧な１皿。 天気のいい日にベヘロフカを舐めながらこれを食べることで優勝できる。

クロアチア：ドブロ（京橋）

Dobro

食べログ Dobro

これも洋食とは微妙に違う。ランチは値段の割に格調高い食事ができる。海産物が推しらしい？ ボリュームは普通。ランチ時間が短いのでアクセスは厳しめ。店の構造がかっこいい。

ハンガリー：パプリカドットフ（白金高輪）

パプリカ ドット フ

食べログ パプリカ ドット フ

また洋食と別物な家庭料理。店名通りパプリカを推している。 味は優しいが、ちょっと印象が弱いかも。豚肉が名物（国宝）らしい。

イスラエル：タイーム（恵比寿）

TA-IM （タイーム） - 恵比寿/地中海料理 [食べログ]

ランチでイスラエル版ケバブ（ピタサンド）みたいなのが食える。よくあるケバブ屋の奴と比べると フムスが入っている、味付けの方向性が異なる、などの違いがある。

イスラエル：デビッドデリ（六本木）

デビッド・デリ （DAVID'S DELI） - 白金高輪/西アジア料理（その他） [食べログ]

羊飼いサラダ（トマトときゅうり角切り）あり。 ミートボールシチューを食べたが、そんなに特徴を感じなかった。 レストランかと思っていたら一階はカフェっぽい雰囲気でスイーツもあったのでその向きの利用もよさそう。

エジプト：コシャリ屋さん

エジプトめしコシャリ屋さん

キッチンカーなので出没地要確認。最近食えてない。 コメ、パスタ、スパゲッティ、豆などの穀物系を雑に混ぜてチリソースとフライドオニオンをゴシャッとした何か。 ほぼでんぷん質のジャンク飯だが満足度はある。プロテインを添えろ。

とりあえずのランチおすすめ：

確率解析すごい

　気まぐれで伊藤積分と伊藤公式を理解したいなーと思い立って いくつかの本を眺めていたのですが、

確率微分方程式入門 ―数理ファイナンスへの応用― (数学のかんどころ 26)

確率微分方程式―入門から応用まで

理学オタクの性として結局行間が気になってしまい、図書館で

確率微分方程式

確率過程入門 (確率論教程シリーズ)

などをチラ見してウンウンした結果、最終的に「アッアッアッこれはやばいやつや…」となって

巨大な憧憬と将来課題が発生してしまったのでその感想文を書きます。（結局以上の本ほとんど読んでない）

　ちゃんとした議論は今後勉強してなんとかやっていく…というか同志いませんか…？

　というわけで、今把握している限りのおおまかな概要を書いてみます。

　測度論的確率論は、可算要素の「かつ、または」をゆるしたBoole的な束構造を持つ事象の集合に、 確率を整合的に（可算加法的に）割り当てることで表現されます。 この事象束をσ加法族といって、通常ある集合の部分集合族として表現されています。ここでは\mathcal{F}と書きましょう。 この束構造を集合演算で表現した空間を可測空間といい、さらに測度が割り当てられているときに確率空間と言います。つまり３つ組(\Omega,\mathcal{F},P)です。ここで\mathcal{F}\subset \mathcal{P}(\Omega)です。

　確率変数とは、可測空間の間の写像で、その逆像がσ加法族の準同型になるものを言います。例えば、X:(\Omega_1,\mathcal{F}_1)\rightarrow (\Omega_2,\mathcal{F}_2)が確率変数であるためには、X^{-1}:\mathcal{F}_2\rightarrow \mathcal{F}_1が束構造の準同型になっている必要があります。 このσ加法族の準同型という構造は、もともと束構造に事象としての意味があることを考えれば自然なことです。 確率変数は可測写像ともいいます。今は実数値の確率変数を考えます。 実数側のσ加法族は、通常開集合を含むようなものを取ります（これをボレル族といいます）。

　実数値確率変数であれば、ルベーグ積分によって期待値を考えることができます。これを \mathbb{E} [ X] と書きましょう。また、一般に条件付き確率、条件付き期待値を、 \mathcal{F}の部分σ加法族\mathcal{G}\subset \mathcal{F}に対して考えることができます。 条件付けにつかう観測が、\mathcal{F}よりも小さい、つまり部分的な観測であることを考えれば自然なことです。 これを\mathbb{E} [ X|\mathcal{G}] と書きましょう。

　確率過程は、適当な時間パラメトライズされた確率変数の族X(t):\Omega\rightarrow \mathbb{R}といってよいのですが、 この場合は時間の経過とともに新しい現象が起きる＝新しく問い合わせ可能な事象が増えていくので、 背後にあるσ加法族自体が時間とともに大きくなっていくと考えるのが自然です。つまり時間順序に従った包含関係にあるσ加法族の族があると考えます。

\{\mathcal{F}_t\}_t,\mathcal{F}_s \subset \mathcal{F}_t \; (s \le t)

　これをフィルトレーションといい、確率過程X(t)がフィルトレーションに適合する、とは、時刻tの確率変数X(t)が\mathcal{F}_tについて可測なこととします。 確率変数X(t)に関する性質の問い合わせが時間ｔ以降には可能になっている、と考えれば自然なことです。

　確率過程を考えるのはもちろん何か表現したり解析したりしたいものがあるからですが、 それらに連続性を期待できる場合があります。そこで連続な確率過程というものを考えます。 定義としては、確率１で(\lambda t.X(t)(\omega))がtについて連続になるようなものです。 さらにここから二種類の確率過程のクラスを考えます。

　ひとつはマルチンゲールといって、 任意の時刻sからのt>sまでの条件付き増分の期待値がゼロになるものです。 つまり、ある意味でフェア、任意の時点から次の瞬間どちらに転ぶかは期待値の意味で50:50であるような過程です。

\mathbb{E}[M(t)-M(s)|\mathcal{F}_s]=0

　もう一つは局所有界変動、つまり任意の時間区間で、変動が有界になるものです。 変動とは、直感的にはその関数が正負にどれだけ動いているかという量です。

|| A(\omega)||_{[s,t]} \lt \infty

　そして確率解析が扱う過程として、この２つが組み合わさったものを考えます。

X(t)=X(0)+A(t)+M(t)

　これをセミマルチンゲールと呼びます。 セミマルチンゲールのこの表式は、実は曖昧さなく決まります。 局所有界変動かつ連続マルチンゲールな確率過程は、定数しか無いことが知られているためです。

　セミマルチンゲールはいわば、「概ねゆるやかに推移していく」A(t)と、「平均ゼロだが激しく震える」M(t)による過程です。 震え、といいましたが、確率過程の「激しい震え」をどのように評価すればいいでしょうか？ マルチンゲールの変分dM=M(t+dt)-M(t)を考えましょう。これは平均すればゼロですが、 分散を計算するときのように、二乗して総和をとったらどうでしょうか？

\sum_i dM_i^2

もし、このdMがdt程度であれば、\sum_i dt^2は細分極限で消えてしまいます。 しかし一般に確率過程では、「激しく震える」部分が蓄積されてのこります。 これは標語的な言い方ですが、停止時間などを駆使することで、マルチンゲールMに対して

\langle M \rangle = \int dM^2

のようなものを定義することができます。これは同一のMだけではなく、一般に

\langle M_1, M_2 \rangle =\int dM_1 dM_2

のようなものを定義することができます。このとき\langle M,M\rangle = \langle M \rangleです。これを二次変分過程と呼びます。

　そして二次変分過程は、局所有界変動になります。つまりマルチンゲールの微小変化を掛け合わせて蓄積すると局所有界変動に戻ってきます。

　さて、様々な文脈で、確率過程で確率過程を積分したい、ということが出てきます。 もし確率過程ではなく関数であれば、これはリーマンスティルチェス積分を定義したい、ということになります。 つまり、関数f,gにたいして \int f dgを考えればよいです。 これはどのように構成したかというと、時間を区分分割して、gの差分とfの区間代表値の積の総和の極限を取りました。

\int f dg = \lim_{|dt|\rightarrow 0} \sum_i f(s_i)(g(t_{i+1})-g(t_i)),\; (s_i\in [ t_{ i } ,t_{ i+1 } ] )

f,gがある程度良い性質を持っていれば、（例えばfが区分的連続でgが連続有界変動） このときの代表値のとり方や区分分割のとり方によらず、細分極限で積分値が決まります。

　確率過程のときはどうでしょうか？ もし局所有界変動であれば、普通の関数のときと同じことを\omegaごとに行えば大丈夫です。 しかしマルチンゲールのときはどうでしょうか？今度は有界変動ではありません。 そして実はこのせいで、同じようにリーマンスティルチェス積分をしようとすると、 被積分過程の区間代表値の選択に依存してしまうのです。 したがって、区間代表値のとり方を固定しなくてはいけません。 これを各区間の左端に固定した結果として伊藤積分が定義されます。

I_M(\phi)(t)=\int_0^t \phi dM=\lim_{ |dt|\rightarrow 0 } \sum_i \phi(t_i)(M(t_{i+1})-M(t_i))

マルチンゲールによる伊藤積分は常にマルチンゲールになることが知られています。

そして、伊藤積分と二次変分過程に次の関係が成り立ちます。

\langle I_M(\phi),I_N(\psi)\rangle(t) = \int^t_0 \phi\psi d\langle M,N\rangle

おわりー！（CV鳩羽つぐ）

　以上はいくつかの本を見て拾った事実の羅列ですが、おそらくピンと来ないと思います。

　そこで、これらの「解釈」、オハナシをしたいと思います。

これ本当は普段（物理とかの）フワッと議論をdisってる身からすると言動不一致じゃねぇかと言われそうなんですが、

　不完全な言い方であることは重々承知である、という但し書きはした、という言い訳をした上で（？）

　あるいは以下の標語的なオハナシが上のように実現されることこそが重要、という立場なんだ、とした上で（？？）

　おもくそフワッとした解釈をしようと思います。許せ。

　マルチンゲールと局所有界変動は、「制御できない純粋なランダム性」と「大まかな挙動」を表しています。 この内、マルチンゲールが問題です。マルチンゲールは微分できません。 先に述べたように、非自明なマルチンゲールは有界変動ではありませんから、 どれだけ短い時間で見ても、ずっと確率的に揺らいでいるために微分が定義できないのです。 しかし現実に確率過程で表現したい系は、何らかの発展方程式を持っていて、つまりどういうわけか「微分」できて、 「制御できない純粋なランダム性」つまりマルチンゲールの、「微分」に毎時影響されて発展しているように見えます。

ここでやりたいことはいくつかあります。

手元に別の確率過程や、あるいは過去の観測結果によって現在の系への働きかけをするためのポートフォリオがあるかもしれません。 それによって、このマルチンゲールを変換ないし、相互作用させた結果を知りたいとしましょう。 これは毎時毎時の相互作用、ないし操作ですから、発展方程式を書き換えることになります。 あるいはマルチンゲールによるノイズ源の影響下で、系の発展方程式自体を提案しているという状況かもしれません。 いずれにせよ、ここでは系の発展方程式に現れる、マルチンゲールの「微分」に、 手元にある確率過程を「掛け算」する、という操作をしたいわけです。 いわば標語的には

\phi(t) \frac{d}{dt}M(t)

が意味をもってほしい。しかし\frac{d}{dt}M(t)を得ることができないので、実際にはこの蓄積

\int_0^t \phi(s) \frac{d}{ds}M(s) ds = \int_0^t \phi(s)dM(s)

を定義することで相応のことを実現するのです。これが伊藤積分です。 つまり伊藤積分は、マルチンゲールの「導関数への掛け算」です。

もう一つ、ランダム性は、例えば熱浴の温度のように、「パワー」があります。 言ってしまえばランダム性の強さみたいなものです。これをどうやって測ればいいでしょうか？ つまり、マルチンゲールの「微分」係数の大きさ(2乗)がほしいのです。 もっというと、「微分」のL2内積がほしいのです。 マルチンゲールの微分は、ある瞬間の、「時間あたり系に加わる確率ゆらぎ」のようなものでしょうから、 もし複数のマルチンゲールがあれば、その瞬間の「時間あたり系に加わる確率ゆらぎの相関」みたいなものが計算できてほしいのです。 これを自己相関にとれば、パワーにほかなりません。 しかしここでもやはりマルチンゲールは微分できない。 そこで標語的に \int^t_0 dM^2,\int dM_1 dM_2に相当する二次変分過程

\langle M_1, M_2 \rangle(t)

を使います。これは標語的に\int^t_0 dM_1 dM_2と言いましたが、これによって本当に実現したいものの気持ちは

\int_0^t \frac{d}{ds}M_1(s) \frac{d}{ds}M_2(s) ds

です。つまり二次変分過程は、マルチンゲールの「導関数のL2内積」です。

それでは、

\langle I_M(\phi),I_N(\psi)\rangle(t) = \int^t_0 \phi(s)\psi(s) d\langle M,N\rangle(s)

という公式は一体なんでしょうか？ これは数式の見た目が内積の記法に似ていますね。 この式がtで微分できたら一体どんな式になるでしょうか？ ここまでにゴタゴタ抜かした「オハナシ」が成り立っているとしましょう。

左辺の微分：

\frac{d}{dt}\langle I_M(\phi),I_N(\psi)\rangle(t)

=\frac{d}{dt} (\int_0^t \phi(s)\frac{d}{ds}M(s) \psi(s)\frac{d}{ds}N(s) ds)

=\phi(t)\frac{d}{dt}M(t) \psi(t)\frac{d}{dt}N(t)

右辺の微分：

\frac{d}{dt}\int^t_0 \phi(s)\psi(s) d\langle M,N\rangle(s)

=\frac{d}{dt} \int^t_0 \phi(s)\psi(s) \frac{d}{ds}\langle M,N\rangle(s)ds

=\phi(t)\psi(t) \frac{d}{dt}\langle M,N\rangle (t)

= \phi(t)\psi(t) \frac{d}{dt}M(t)\frac{d}{dt}N(t)

！？

自明では？？？？？？？？？？

というわけで確率解析をやりましょう(同志募集中)。

ベクトルバンドルのリー微分

先日 http://www.asahi-net.or.jp/~fu5k-mths/pdf/bundle_lie_and_noether.pdf

を書いたのですが、ベクトルバンドルのリー微分だけ抜粋します。

解析力学は学科ではドチャクソ重要な理論で、それは場のバージョンでもそうなのですが、 物理学では往々にして

「～という議論ができるんですよ（シンプルなコア議論）」

↓

（永遠の開き）

↓

「あの時のコア議論をここで応用します。こんなアナロジーができますね～」

ということが発生するのですが、

そのアナロジー全然自明じゃねえよ

という気持ちになることがあり、場の解析力学はそういう例の一つです。あとグラスマン数の経路積分とか… 基本的なパターンをやっとけば、その任意の変種がいつでもwell-definedでしょみたいな…願望でものを語るのをやめろ… 場のハミルトン形式もアレですよね…まぁあのくらいは汎関数微分とかをきちんと書けばなんとかなるかもですが…

で、長年場のラグランジュ形式の何が不満だったかというと、 Noetherの定理がクソほどもわからない…「場の理論　Noether」とかでググってもらえると、 いろんなのが出てくると思うんですが、だいたい「次の微小変換を考える」とか言ってこんな式が出てきます。

\displaystyle{ x\mapsto y = x + dx \\ \phi(x)\mapsto \phi(y)=\phi(x)+d\phi }

は？？？？？？？？？？？？？？？？？

ってなりませんか？僕はなったし、これだから動的型で数式書くやつは何をやっても（ｒｙ

物理学者が場の量書くとき、だいたい型書かないじゃないですか、まぁそれは珍しくないんですけど、 場の量が何から何の関数なのかわからんし、xって時空点なのか、座標なのかもわからんし、\phiって成分なのかベクトル値なのかもわからんし、故に変換というのが座標変換なのか幾何的な能動変換なのかもわからないし、 まず\phi(x)って書いたときに、\phi(x)を値まで評価したものが移されるのか、\phi,xって記法が何らかの量化制約を持ってるのかもわからんわけです。 ちなみにわかった今だからいいますけど、これ本当はここで場の量(バンドルセクション)である\phiって記号が登場しちゃいけないんですよ。この変換は一義的にはセクションの変換じゃなくてバンドル自体の変換なので。

それで、これが一体なんなのかわからん限りには、場Noetherがなんであんな形しているのかもわからんわけです。これがベクトルバンドルの自己同型変換の無限小版として完全に幾何的な能動変換として書けることに気づいてブチ切れたので、以上のノートを書きました。

結論からいうと、ベクトルバンドルの自己同型変換生成子みたいなものを定義することができて、それは上のようなものをちゃんと定めるし、Noetherの定理はそこから出てくるものです。

まずベクトルバンドルを定義する必要があるのですが、wikipediaを見て。

ベクトル束 - Wikipedia

各点にベクトル空間がついてて、局所的に成分表示できるようなもの、と認識してください。 ここで「なんや、単なる多成分場やんけ」と思うのはやめてね…多様体がいつでも\mathbb{R}^nの同次元部分集合と思うが如き…

いや実質局所的にはそうなんですが、我々はいま解析力学をやっていて、解析力学は座標普遍であることを散々強調するわけです。じゃあちゃんと自明化写像によらないということ、それがどういう意味でかというのをきちんと述べるべきであって、多様体の多の字も出ない教科書は滅ぼすしか無い…

で、バンドルというのは、基本的に底空間への射影\pi:E\rightarrow Mというのも持っています。 なので、ベクトルバンドルの射がこれについての可換図式を満たすことは自然なことです。 底空間の写像にファイバーの行き先が整合的であるということですね。

そして先の謎\mapstoは、まさにこの可換図式なのです。\phiが出てくるのは間違った書き方と言いましたが、正しい書式はこう。

\displaystyle{ g:E_1\rightarrow E_2\\ v\in \pi^{-1}(x)\mapsto g(v)\in\pi^{-1}(f(x))\\ f:M_1\rightarrow M_2\\ x\mapsto f(x) }

\pi^{-1}(-)は射影の逆なので、各点ファイバーです。これなら秒でわかる。型注釈、所属集合注釈を惜しんではいけない。

ほいで、では場Noetherはなんだったのか、という話になるんですが、要するにリー微分なんですよね。

これは有限次元ラグランジュ理論の時もそうで、自由度空間に対する変換があって、そのリー微分が、 ラグランジュ方程式比例項とNoetherモーメントの微分で書ける、というのがNoetherの定理なのです。

ところで、ベクトルバンドルのリー微分ってなんでしょうか。なんか上手い定義が必要です。 一番馴染みあるベクトルバンドルといえば、ベクトル場、テンソル場、微分形式ですね。 これらには多様体の１パラメータ変換群（の生成子）があれば、リー微分が定義できます。

f:M\rightarrow Nが多様体の可微分写像としましょう。これの微分がベクトル場のなすベクトルバンドルの射を決めます。それは次のようなものです。

\displaystyle{ df:TM\rightarrow TN\\ v^i\partial_i \in TM_x \mapsto \frac{\partial f^i}{\partial x^j}v^j \partial_i \in TN_{f(x)} }

これはfを座標空間に引き戻してからそれで微分した微分係数を使いますが、座標によらず定義できます。 これが無限小だとしましょう。十分小さな[tex;\epsilon]を用意してfの座標表示がx^i\mapsto x^i+\epsilon X^iとなります。 X^iはこの変換の生成子です。するとベクトル場の成分変換は

\displaystyle{ df:TM\rightarrow TM\\ v^i\partial_i \in TM_x \mapsto \left(\delta^i_j+\epsilon \frac{\partial X^i}{\partial x^j}\right)v^j \partial_i \in TM_{x+\epsilon X} }

これはベクトルバンドルの微小変換が \frac{\partial X^i}{\partial x^j}のような行列で実行されていることを意味します。

しかし、これは変換規則がファイバーの自己変換のようにはなりません。\partial_iがあるせいで、場所に依存する自明化の変換を施すと 変換行列の微分項がでてきます。

逆に言えば、これを組み込んだ変換規則をもつような行列を考えれば良いことになります。ベクトルバンドルの変換なので、 底空間をどれだけ動かすか、という底空間のベクトル場と、ファイバーの成分変換行列の直和で、バンドルの局所自明化ごとに与えられるものを考えます。

\displaystyle{ \{(X,M_a)\}_{a}, X \in \Gamma(TN_{U_a}),M_a\in \Gamma(U\times \mathbb{R}^{n\times n}) }

ここで、a\rightarrow bのフレーム変換行列：つまりGL(n)値場\Lambda:U_a\cap U_b \rightarrow GL(n)に対して、 次のように振る舞うことを条件に課します。

\displaystyle{ (X,M_b)=(X,(X\Lambda)\Lambda^{-1}+\Lambda M_a \Lambda^{-1}) }

ここでXは微分として作用しています。これを課すことで、自明化によらないベクトルバンドルの微小変換を実現します。 では実際にリー微分しましょう。リー微分は、場の量に対して、ある点の値を無限小変換で別の場所に持っていき、行き先にすでにあった量との比較をします。 V\in\Gamma(E)をベクトルバンドルのセクション、つまり場の量としましょう。局所標構（基底ベクトル場）e_iを使って、V=v^i e_iとなっているとします。

\displaystyle{ v^i(x)\mapsto v^i(x)+\epsilon M^i_jv^j(x) } から \displaystyle{ v^i(x)\mapsto v^i(x+\epsilon X) } を引いたものなので、一次のオーダーで、 \displaystyle{ -(Xv^i)(x)+M^i_jv^j(x) } がベクトルバンドルのリー微分となります。実際、Mの変換規則が、これをwell-definedにしています。

あとはノートを参照してください。

やっておいて気になっているのは、物理学者が一体場の量をなんだと思いっているのかということです。 実のところ合意がないような気もします。僕はベクトルバンドルの概念が気に入っているので、それだと思っているのですが、 本気でただの多成分場と思っているのかもしれない。つまり大域的自明化が可能な。

しかしその一方でゲージ場などで自明化によらない云々というのを後付けで導入したりもします。 ただゲージ場はゲージ群なので、一般的なフレーム変換ではないというのはありますが…

ギターキット/Elm/就/...

1.エレキギターを取得しました。

　高品位なオーディオを吐くDAWやシーケンサがいくらでも手に入る今、なぜ人は楽器なんて面倒なものをやるのでしょうか？？？？？？？ 音楽が情動のメディアであるように、楽器も一種のメディアなのかもしれません。肉体と音の間の。 とりあえず人間には可制御な物が増えると精神に良いという経験則があります。リアタイだとなお良い。

　そんな訳で、そこそこ取り回しの良い楽器というのが手慰みでほしくなるのですが、これには様々な制約が存在します。 当然のように集合住宅に住んでいますから、生楽器はアウトです。 僕は相対音感はともかく絶対音感が極限まで壊滅的なので音程がアナログな楽器はダメです。 ほいで音域が辛いのもいやだし、コードも弾きたい。さらに左利きなので鍵盤が全体的に辛い、となるとエレキギターになります。

　というのはこじつけで、単に友達がギターもってて僕も欲しいなーと思っただけです。 このように人は思い出すついでに様々な文脈を捏造できる。

　僕は仕組厨なので自作厨をしばし合併症として発症します。 で、Googlingするとギターキットというのがあり、無塗装ボディにバラバラのパーツがセットになったやつが出てきます。 はい、君に決めた。

ammoon 未完成のDIYエレキギターキット バスウッドボディー ローズウッド指板 メイプルネック特別デザイン ヘッドストックなし

なんかHOSCOとかいうメーカーの作例は結構転がっているのですが、 こっちのメーカーまだ新しいのか全然でてこない... 販売元は深センっぽい？　まぁ製造も中国でしょうね。 ちなみに決めた理由はヘッドレス/24フレット/３PUあたりです。 軽い/音域広い/音色広い、といったとこでしょうか。ミーハーですね。で、その結果。

f:id:phykm:20180509203725j:plain

　塗装は...めんどい...今度で...

　新興中華キット（？）ということで、まぁ様々な事象がありました。

　まずボディーにピックアップ３つとブリッジを固定するんですが、 ピックアップ２つとブリッジが入らないんですよね。サイズ的に。 ボディーにこう、くぼみを入れるの、なんか座くりとか呼ぶらしいですが、 座くりのエッジが甘すぎて、四角い形のダブルコイルピックが普通に入らない... シングルコイルピックもなんか妙に膨らんでいて入らない... さらにブリッジもサイズがギリギリ過ぎて入らない... これフローティングブリッジ（バネで弦張力と釣り合わせているだけで固定されていない）の一種なので、 本当は可動範囲だけの隙間があかないといけないんですが...。 まぁそういうのもあるさ、とカッターとナイフとリューターでゴリゴリして入れました。

　しかしブリッジにはもう一つトラップがあり、そのままつけるとなんと弦長が足りない... オクターブチューニングできません。しかたないので、更に座くりを広げて少し下につけました。

f:id:phykm:20180509203742j:plain
道具がないのでカッターとリューターで削ったことによる手作り感

それから、ネック先端に弦をロックするテールピースがぴったりつかない...同等品の

https://www.amazon.com/ammoon-6-string-Headless-Electric-Locking/dp/B01N6C99RU

にまさにそういうトラップによる悲劇が書かれており、とりあえず噛み合うまで削りました。

　 　回路ボックスのフタがネジ止め式ですが、明らかにネジ穴の位置を間違えている...

f:id:phykm:20180509203755j:plain

　これ、止めてある二箇所には最初穴が空いてなかったんですよ。空いている二箇所はよく見ると穴の向こうが虚空で、 要するにネジが刺さるための土台が無い...。まぁこの程度は別にどうということは...

いやさすがに組み立てればわかる欠陥ばっかやんけ、ちゃんとチェックして、どうぞ。

　 　ギター組み立てのネックは、いろいろ調べたところ、まさにネックらしいのですが、 キットについてここだけはちゃんとしてました。ボディとネックがめちゃくちゃタイトに刺さる。 ネック角度が甘いと弦が指板から落ちるなどの致命的な欠陥になるのですが、そのようなことは起きませんでした。

　演奏感ですが、ウーン、よくわかりませんね（ギターが弾けるとは言っていない）。 実際Youtubeなど探すと、安ギターと高級ギターの音色比較、みたいな動画も結構あって、 見てみると、たしかに高いやつのほうがくっきり鳴ってる気はするな…？という感じはありますが、 いかんせん楽器の特性上エフェクターとかでいろいろ変わるものだし、 それらと比べてこの素組みギターがどうかというのはよくわからない... というかそもそもエフェクターもアンプももっていないので、 現状オーディオIFでDAWを通してディストーションをかけるという遊び方になっており、単純比較が困難。 塗装したらまた音色変わるかな？

　いまのところ音域広いし、コンパクトで弾きやすいし、不満はないですね。 自分で組み立てたということで、ギターの勝手もわかり、 なんか起きてもまー作った時みたいに改造すればいいやとなる心理的障壁のなさもよい。 エレキギター、もうとにかくただのアナログ回路なんですよね... 要するにアナログ回路わかっていれば無限に改造できるという...

　エレキギター自作勢というのも特に海外などに一定数存在するようで、 Amazon.comとかだと普通にもっといろんなメーカーがバラパーツを売ってたりします。 弦張力に耐えるられる程度にボディとネックをつなげて、 ナットの調整範囲内で弦をまっすぐつければ何でもギターになる。 あとはピックアップだけギター用のやつを買って、出力はアナログ信号処理、という流れなので、 いい感じにアマチュアにも届く技術水準といえます。

　 　いずれ改造にも手を付けたい。

2.Elmに入門しました。

　以前HasteとかいうHaskellによるAltJS？を触ったのですが、またHaskellっぽいJS？をちょっと前に知りました。 正確にはJSではないのですが...

home

はじめに · プログラミング言語Elmの薄い本

まんまHaskellやんけ。

　いや、ところどころ違うのですが（後述）、一般構文は殆どHaskellとかOCamlのそれですね。REPLすらある。 最大の特徴は、これは汎用プログラミング言語ではなくてDSLで、 The Elm Architectureに従ってWebページを記述するのに特化している点でしょう。 プログラムのエントリポイントの型がそもそも独自のものに決められていて、 それが要求するフィールドを定義する、というスタイルのようです。 コンパイルするとページをまるごと吐くので、HTML/JS/CSSの一石三鳥（ほんとか？？？？？？？？？？）

　 　このThe Elm Architechtureというのがなかなか洗練されており、かなり抽象度の高いことができます。 Hasteは単にJSがHaskellで書けるだけだったので、ページ要素の操作はまんまIOで、 コールバック登録もIOとかで、要するにMVCみたいなことをやろうとすれば全部自分でやる必要があるのですが、 Elmの場合はそのへんも抽象化されており、コールバックの「登録」みたいな操作はしません。定義はしますが...

とりあえずこんなん書いてみました。

http://www.asahi-net.or.jp/~fu5k-mths/elm/elm_block/index.html

入門してみた所感としてThe Elm Architectureの「直観」を描いてみたいと思います。

f:id:phykm:20180509222522p:plain

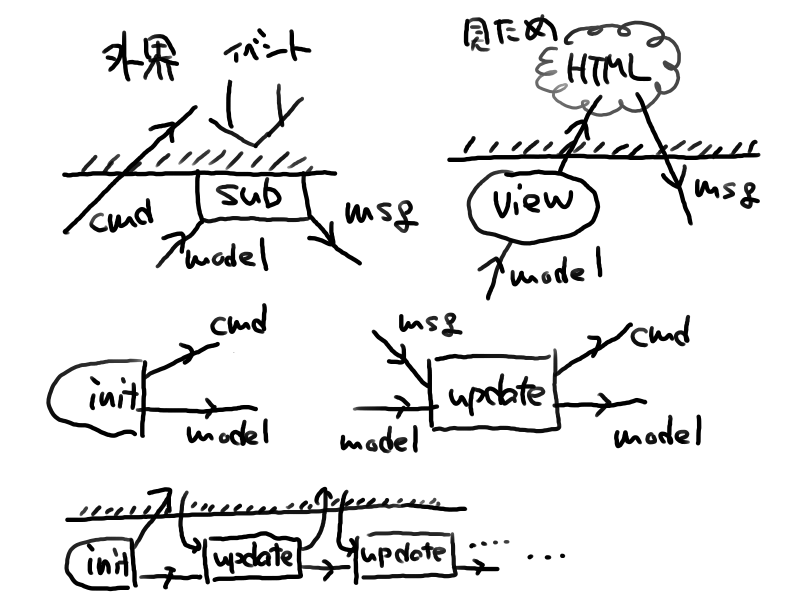
無理。

なんか紐図( https://arxiv.org/abs/1401.7220 とか)っぽいものができる気がしたが気のせいだったぞ！！！！！！！！

文で書きます。基本的には代数的データ型を駆使して、MsgとModelという型を定義し（これは本当になんでもよい）

init:(Model,Cmd Msg)
update:Msg->Model->(Model,Cmd Msg)
subscription:Model->Sub Msg
view:Model->Html Msg

を定義すれば一丁あがりというものです。

型を適当に解釈できれば、この仕様のイメージがつかめます。

Modelは定義するWebページの内部状態、

Msgは内部のメッセージングです。

Cmd aはメッセージaに基づくコマンド、

Sub aはメッセージaを吐くかもしれないリスナー、Html aも同様にaを吐くかもしれない文書です。

このとき、 定義するフィールドはそれぞれ、 init:初期状態と初期化処理 update:Msgに応じた状態更新と副作用 subscription:Modelに応じたリスナー view:Modelの見え方 と解釈できます。

　Msgはクリックやキーボード、時間経過など、Webページが識別してほしいシグナルを直和などを使って全て書き下し、 ModelはWebページが把握しておいてほしい全ての情報を直積やリスト化などで書き下すことで定義すればよいです。 状態遷移などで把握すべき情報が変わる時はそこを直和にする。オートマトンっぽい。

　Msgがどこかから吐かれるたびに、updateが呼ばれます。updateは起きたことに基づいて状態を更新して、 ついでにCmd Msgで何か仕事をできます。状態は常にviewで表示されます。

上のコードは

github.com

にあります。ていうかゲームプログラム難しすぎるのでは？？？？？？？？？？？？？？？？？

　状態としてReady、または　Game (ボール状態とブロック、終了フラグ)、 メッセージとしてクリックとマウス移動を取っています。 描画に用いているCollageというパッケージはCanvasベースらしいので、できること/性能もそれに準じたものと思われます。 あんまり複雑なのをやるとつらそう。ただWebGLのパッケージも存在するっぽい。

Elmの開発環境（？）は結構整っているように思えます。とりあえず公式から処理系をインストールし、

サンプル

examples

をみながらやりたいことを考え、

Elm Packages

で必要なパッケージを調べます。必要なパッケージがわかったら、 elm-pachage install を必要なだけ打って、インポートし、書きます。

　どうも開発ディリクトリに非標準パッケージを直接DLしてくる(elm-stuffというディリクトリができる)っぽいので cabal hellみたいなことは起きにくい？　ページ自体はちょっと重め。

　REPLもあるのでこれにロードして関数をチェックすることもできます。 できたページを確認するのにコンパイルしてもいいですが、elm-reactorとかいうドチャクソ便利なものがあり、 これを起動するとローカルサーバーが立ち上がって.elmファイルを直接ブラウザから見れるようになります。ソースファイルを選択すると、 ファイル生成なしに、サーバーがコンパイル後のページを返そうとします。

　エラーがあった場合にはエラー文もブラウザで見えます。地味にコマンドラインよりも見やすいので助かりがあります。 ブラウザをリロードすれば再コンパイルします。

Haskellと微妙に違う、といいましたが、気になった点としては以下です。

  • Cmd Subのような->みたいなカインドはあるが、型クラスはない。
  • ::と:が逆。
  • リスト型は[a]じゃなくてList a
  • 型定義が基本typeかtype aliasだけでスッキリしている。もちろん前者にコンストラクタが要る。
  • 実感は無いが、正格評価らしい？
  • トップレベルのパターンマッチができない（？）。case of で頑張る。

最後のは表現が正しいのかわかりませんが、要は

sum::List Int->Int
sum [] = 0
sum (x:xs) = x + (sum xs)

じゃなくて

sum ls = case ls of
    []     -> 0
    (x:xs)-> x + (sum xs)

としろということです。

感触は結構いいのですが、これ本気でCSSデザインやろうとしたらどうなるのか... 一石三鳥だが要するに三鳥分定義を書かなきゃいけない点は変わらず... あと言語の方向性からして厳しいとは思いますが、他JSやCSSライブラリと連携取れるんだろうか...

なんか来月に日本語の解説書が出るっぽい。

基礎からわかる Elm

当然のごとく予約しました。

3.就をやっている。

就をやっている。助け...

4.論をやらなくていいのか

やばい。

語学嫌いは言語類型論をやれ

　半年たってしまった...

　皆さん、英語（任意の語学）好きですか？

僕は嫌いです。

　人はなぜ、特定の教科/分野/学問を好きになったり嫌いになったりするのでしょうか。 精神論や観念論はよろしくないという立場においては、これは端的に言って 「好き/嫌い」と判定されるような行動をとる傾向性を、 適当なフィードバックで強化されるような環境に置かれたからでしょう（身も蓋もない）。 そのような話として行動分析学があるので興味ある向き、そして教育者各位は読んで僕に教えてください。

行動分析学入門―ヒトの行動の思いがけない理由 (集英社新書)

行動分析学入門―ヒトの行動の思いがけない理由 (集英社新書)

行動分析学入門

行動分析学入門

  • 作者: 杉山尚子,島宗理,佐藤方哉,リチャード・W.マロット,アリア・E・マロット
  • 出版社/メーカー: 産業図書
  • 発売日: 1998/03/30
  • メディア: 単行本（ソフトカバー）
  • 購入: 3人 クリック: 30回
  • この商品を含むブログ (17件) を見る

　思えば語学の成功体験なんも無いですね。僕は理系か文系かというとド理系で、 ここ数年で偏見が緩まったおかげて人文/社会科ももしかしたら面白いかもしれないと思いつつありますが、 語学は銃口を突きつけられないとやらない位にモチベーションがない。 中高大と語学はとにかくもう、

こういう表現がある、こういう語彙がある、 書いて覚えろ、聴いて覚えろ/書き取れ、 （どうでもいい文を）読んで読解しろ、

という話ばかりで、 原理さえ押さえればどんな議論を考えてもよいという高い自由度/正誤判定が一貫していて容易という明快さがある数物に比べて、 なんだこのクソつまらん教科は、教科じゃないんじゃないか？などと思ったりしました。 あと僕は耳も悪いので日本語も英語も文脈抜きで単語や短文をクソ音質で投げられても聞き取れる訳がない。

　今でも「言語学」はともかくとして、「語学」は学問じゃないよな、と思っています。 どちらかというと体育や美術に近い。というのも、それは追求したり分析したりするものではなくて、 習慣化したり、表現したり、交流したりする為のものなので。 しかし体育や美術、つまりトレーニングや表現技法の一種なら、 それはそれでゲーミフィケーションやコミュニティによる動機づけがまるで足りてないのではないか。 なぜ日本の英語話者は日本とかいう環境で英語を学び通せてしまえたのか。 まぁこの教授形態の愚痴は本題でないので置いておきます。 学校教育に期待できないのは今に始まったことではない...

　ともかく語学はクソつまらない。面白いと思っている人には申し訳ないですが、 英語が覇権を握ったが為にどの分野で大成するにもこんなつまらんものと付き合わされる羽目になった歴史を恨みざるを得ない。 なぜ面白くないのかというと、その内容や事実に内的説明が殆ど与えられないからです。 ただ規則と事実が、何故こうなっているのか、なぜこうすると良いのか(何の為なのか)抜きの羅列になる。 これが数物であれば、原理はなるべく一貫性とコンパクトさを保とうとしますし、各種公式や定理にも、 それを考える動機づけ、ないしなぜそれが成り立つかの導出が伴っています。 今にして思えばこれは当たり前で、特定の言語なんていうのは、 歴史/文化的経緯でフワッと決まった側面を持っているわけで、 まったく普遍的でも必然的でもない要素が多分に含まれているのです。 そんなただの偶発的な事象に由来する取り決めに「親しむ」ことを強いられるのが気持ちいいわけがありません。 多様な文化はどんなめちゃくちゃなものも存在は尊重しますが、それは僕に（誰にでも）強制しないという条件があります。

　なんかもっと普遍的で、汎用で、形式的側面から言語をなんとかできないのか... 学部の時に形式言語理論に潜って文脈自由文法とその派生(言語学では句構造文法というようですが) に出会ったときの感動が想像できますでしょうか？英語はもはや何も分からんが、これなら分かる。 なぜ語学教育は近似的でもいいから句構造文法を一番最初に提示しないのか??????? 人を馬鹿にしやがって。許さんぞ。今でも思っています。

　さて、去年に遡りますが、こうして悶々としていたなかで、ある分野に出会います。 普通の教育課程をパスすると英語とかいう憎き覇権言語が外国語の9割になってしまいがちですが、 当然ながら世の中には大量の言語があります。英語や日本語とか似ても似つかない言語もありえます。 しかしwikipediaを眺めていると、ある言語は◯◯的で～とかある言語はこの言語に似ていて～/違って～とか、 あるいは品詞や句や節や諸々の語学概念が、複数の言語にまたがって、あるいは比較されて用いられている事がわかります。

「まてよ、そもそも言語学（？）には、こうした言語によらない概念や語法や道具立てがもっとあるのか？」

と思って調べていくと、どうも言語類型論という分野がある事がわかります。 それらしい読み物や入門書が参考文献として出てきます。

言語のレシピ――多様性にひそむ普遍性をもとめて (岩波現代文庫)

言語のレシピ――多様性にひそむ普遍性をもとめて (岩波現代文庫)

言語類型論入門――言語の普遍性と多様性 (岩波オンデマンドブックス)

言語類型論入門――言語の普遍性と多様性 (岩波オンデマンドブックス)

言語普遍性と言語類型論―統語論と形態論 (言語学翻訳叢書)

言語普遍性と言語類型論―統語論と形態論 (言語学翻訳叢書)

ｳﾞｫｯｯｯｯｯｯｯｯｯ

　これは大当たりでした。僕は語学弱者であり、言語学専攻でもないので、誤読の可能性は大いにあるのですが、 ここ数年で最高レベルに分野の存在に感謝を捧げています。

　いいですか？リンクは貼りました。 とりあえずリンゼイの言語類型論入門をカートに入れてください。話はそれからです。僕もこれを今読んでいる。

　何が当たりだったか。この分野には、 「語学がそれ自体面白いものである為には足りないと思われるもの」の大半が入っていたからです。 それは何かというと、言語（特定のものではなく全ての）それ自体に対する説明としての科学です。 リンゼイでは次のように類型論を定めています。

言語の全体像やその構成部分の分類を、それらが共有する形式的特徴に基づいて行うこと。

　言語全体を相手にしているので、自ずと語法は特定の言語を贔屓しない中立的なものを志向します。それから、主に形式的特徴に基づくことで、例えば地理的、歴史的経緯による系統よりは、その言語が言語として持つ性質にフォーカスします。このあたりの傾向を通言語的とか共時的とかいいます。

　リンゼイ本に沿って、具体的に類型論が何を語るか少し見てみます。

　まず品詞はありふれた概念ですが、通言語的に品詞という概念が意味を持つか、という問題があります。 品詞なるラベルは何で決まるのか？それらの判別規準はなにか？というのをあらゆる言語に通じる形で定めようとするのは難しい、という話が延々とされます（誠実ですね）。おそらく大抵の言語に名詞動詞形容詞等etc...といったカテゴリーがあること自体はいいでしょう。そこで、次の普遍性が提出されます。「すべての言語にて、名詞動詞は《開いた》品詞で、形容詞以外の他の品詞は《閉じた》品詞である」。ここで、「開いた」というのは、語彙の追加や削除が容易に起きることを指します。これはちょうどプログラミング言語のコア部分はそうそう変わらないがライブラリは随時追加されるような様子に似ています。

　もう一つ有名な例をだします。それはSVO要素の順序についでです。そもそもSVOに相当する概念が各言語にあるのか/それは何で系統的に識別できるか、という問題がありますが、 ひとまずこれがあるとしましょう。例えば英語はSVO、日本語はSOVです。 理論上あり得るSVO順序６種類のうち、このSVO/SOVを採用する言語が大半であり、VSO/VOS/OVSは稀、OSVは全く無いという統計が存在します。 そしてこれは何故かというのを、認知上の利点、統語的なVO要素の結びつきによって説明します。 例えば、Sは先行した方が認知上メリットがあるだとか、VOは動詞句を構成するのでこれが分割されることは稀、というように。

　それから、これはベイカー本でも紹介されているのですが、多くの文法で、動詞句のVとOの順序は、 それ以外の句、節の構造、修飾詞、冠詞の参照先の順序、前置詞/後置詞の傾向などと相関があるという指摘が入ります。 これに関する説明や概念立てを検討した後で、ドライヤーの方向分岐理論が紹介されます。 方向分岐理論の説明がいまいち飲み込めないのでここはちょっと自分の理解ですが、それは 「構文解析木の分岐において、複雑さがバウンドされないカテゴリ（分岐的カテゴリ）を左右どちらに置くかは一貫している」と読めます。 もっと大雑把には、言語の文法は右再帰か左再帰かを統一する傾向にある、と言って良いのではと思います。 VO順の場合は、Oは複雑な構造を持ちえるので、動詞句以外の句などにおいても、左側にそうした複雑な要素を置こうとします。 そして、この理由はなぜかと聞かれれば、もちろん構文解析の容易さを挙げます。

これ滅茶苦茶面白くないですか？？？？？？

　他にもいろんな分析例があるのですが、どうも目次をみると、これは言語が果たすべき基本機能やレパートリーが概ね共通で、それをどう実現するかという(制限された)多様性をコンパクトに列挙しているようにも見えます。つまり、類型論は

  • あらゆる言語全体という集合にも、かなり強い制約や共通した性質がある(普遍性）。

  • 言語がある機能を実現する為にとる手段は、限られつつも選択の余地がある(多様性)。

という二点を明らかにするのです。この普遍性と多様性はまさりリンゼイの副題です。

　前者の普遍性は、なんらかの尤もらしい説明が与えられます。 　後者の多様性は、限られつつも恣意的であることが了解されます。

　例えば、ある人が新しい言語を学ぶとしましょう。もし十分な類型論的知見があれば、 その言語の文法のうち、どこまでが言語によらない必然的な要素、つまり一貫した説明を与えられる部分で、 どこまでがその言語の恣意的な選択、つまりそうである理由は無いが、その言語「らしさ」を成す部分であるかを了解できるわけです。

　こういう話が学習段階で提示されたらもっと語学が好きになれたろうにと本当に思います。

　大事な違いですが、例えばこれはある語の語源がどうとか、歴史的な語族系統図がどうとか、◯◯語圏の文化と言語の関係がどうとかそういう話では全く無いんですよ。むしろ全く逆で、そうした雑多な要素を一切排除して残る形式的なコア部分のその原理と選択肢は何か、という話なのです。（なんか雑多で非形式的で豊かであればあるほどいい、という文化系特有の傾向（偏見）、はっきり言って大ッ嫌いなんですが、まぁそれはおいとくとして）　個人的な性癖ですが、こう、習うより慣れろというのが本当に無理で、もっというと疑うよりも習えというのも厳しいのですが、こうやって普遍的な部分からスタートして、残りの恣意的な部分は、それこそが◯◯語なんですよ、と言ってくれれば、とりあえず説明の要求は前者に集中して、後者はまぁそれこそが◯◯語なんだから仕方ないよな、と思う余地が生まれるわけです。

　プログラミング言語のような人工言語は、ある種の表現力を実現するためにその構文を考えていると思います。 であれば同様の「この機能を実現するためにどの構文をつかうか」という視点が自然言語にもあって然るべきではないですか。 自然言語の機能のレパートリーは、どうも歴史を通してあまり変わっていないようなので、 各々の言語はそれをどうやって実現するかという、制限された選択肢のなかから、あるやり方を一貫して選んだものだといえるわけです。

　どうですか。ここしばらく類型論のプッシュばかりしています（研究をしろ）が、ちょっとでも興味をもったらリンゼイをポチってください。僕はリンゼイが済んだらコムリーにいきます（研究をしろ）。

　 　なお申し添えますが、言語類型論をやっても個々の言語が出来るようには全くならないと思います。

環、有界、STモナド

全部話題バラバラです。

1.なぜ物理量は環なのか？

　今ゼミでIsham某量子論本を読んでいたりするのですが、これに限らず、ある文脈において、次のような対比が語られる事があります。 すなわち、

古典力学では物理量のなす環構造が可換であったが、量子論では一般に非可換になる。

　この可換非可換という対比は、単にある種の代数構造の条件開放という意味で「少なくとも数学的には」自然な一般化の発想で それで例えば可換/非可換C*環が、GN双対を通じて普通の幾何(コンパクトハウスドルフ位相空間)/非可換幾何の対比になるだとか、 あるいは量子群だとかいう名称がここに由来するだとかいった話に繋がったり、物理では非可換性によって、物理量の同時測定、同時値付与ができない、不確定性関係につながるとか、そういった風潮や言い回しの背景を提供しているようにに思います。（そうでないならそれは良いことなのでどうでもいいです）

　しかし、ほんとかよ？　毎度のことですが、この手の言説の雑さ加減、ちょっと反省してくれというお気持ちが湧いてきます。 　いや、数学的な構造それ自体に興味があるので、可換非可換を対比しますというのは別にいいんですよ。それは自由にやればいいし、 やっていきをした結果として理論物理に有意な構造が手に入ればそれを使うのもいいですが。 　問題は、物理学の基礎や定式化において「量子論は物理量環が非可換になったやつ」という言説が目に余るということです。

　まずそもそもですが、

定式化段階で「物理量が可換環である」とみなせる理論、そんなにあるか？

という点です。大体において、こういう状況での可換環というのは力学相空間X上のC(X)のことを指しているはずです。 要するに、「力学的相空間/状態空間があって、物理量がその上の複素数値関数で、各点積による可換環構造をもつ」というビジョンは 古典力学ではありがちだよね？ということを想定して、古典物理は可換C*環だ！といっているのです。

　はー、ちょっと待てよと。例えば学部でやるような以下の古典理論を見てみますよ？

  • 解析力学(L)

    • ラグランジアン：TN上\mathbb{R}値関数、加法的、\mathbb{R}mod、しかし乗法的でない。
    • Noetherモーメント：リー群が作用しているとき、リー代数からNoetherモーメントの対応はTN上\mathbb{R}値関数へ線形、乗法的ではない。

  • 解析力学(H)

    • ハミルトニアンベクトル場：\mathbb{R}mod、乗法をもたない。
    • poisson環：\mathbb{R}mod、乗法を持つが可換ではない。

  • 古典場理論(電磁気,流体含む)

    • 電磁気の各種量：基本変数がベクトル場や微分形式なのでいずれも\mathbb{R}mod、乗法はない。外積はgradeを上げる上に可換ではない。
    • 物理量として、密度関数の領域積分や、あるいはその密度関数自体を取るので、そもそも乗法は限られた状況でしか入らない。(例えばエネルギー密度の計算やポインティングベクトル場など)

  • 熱力学

    • 熱力学関数：状態空間上の実凸関数だが、同次性を持つことを強いられるので、乗法を無制限にとれない。系の拡大と加法が取れるので\mathbb{R}mod。

  • 相対論

    • 古典場の理論に準じる。大体テンソル場およびその領域積分が基本的物理量なので、乗法は無制限にとれない。

　実数値関数ばっかやんけ！というツッコミをおいておいても、殆どが\mathbb{R}modであって、 \mathbb{R}algじゃないわけですよ。algebraっぽい奴だって各点積とは違うし。 いや、それでも解析力学で、任意の物理量としてTN,TN^*上関数環の、poissonではない各点積関数環を考えられるでしょ、 と思うかもしれません。しかしそれにどんな物理的意味がありますか？poissonはハミルトニアンベクトル場の無限小リー微分としての 意味がありますが、各点積はなんですか？ええ？なんもないでしょう？　 第一ですよ、環構造を定義する方法なんて、今やいくらでもあるわけです。集合が手に入ったら適当が環を持ってきて関数環、形式的積を定義して自由生成、結合的演算があったらそれで環とか、数学的構造が手に入ったらまぁご自由に作ってくださいと。 そんななかで大事なことは、（物理において）「その積が物理的動機にモチベートされている」かどうかであって、 その意味でいえば相空間複素関数環の各点積構造、ほとんど動機がないわけですよ。 解析力学で各点積関数環を作れるのは、単に「作れてしまう」から計算や試案に便利というだけであって、 それ自体に統一された第一級の物理的な解釈があるわけではないのです。

　こうしてみると、ガッツリ環として最初から宣言しているのは、ハミルトン形式のPoisson環くらいで、 これは最初から非可換なわけですから「量子論では物理量は非可換！」とか「？？？？」じゃないですか。 大体角運動量の議論とかですら、リー代数->正準力学系->ユニタリ表現で、非可換な代数が準同型になることを使っているわけで、 それをスルーして、「非可換性を強調するときだけC(X)、実際の運用の時はpoissonにアナロジーを求める」なんてダブスタもいいとこです。いい加減にしろ。

　これ結構悪影響があって、というのも量子力学では物理量は作用素で表現しますが、 まぁ案の定「作用素」ですから、環になりますよね？ そして「量子物理量の環構造の物理的意味が不明」という問題が発生してしまうのです。

　しかしまってくれ、そもそも環構造に物理的意味が最初から憑依していたケースは、そもそも古典物理ですら限られているわけで、 その古典物理の物理量環だって、「相空間があって、値が実数値だから定義できる」という意味しかない。 だからこの意味不明問題は、そもそも定式化がナンセンスであって、積構造に何を期待するかというのは、 ヒルベルト空間の作用素という数学的モデルの実装戦略を採用した我々が最初に動機づけすべきことなのです。 で、それがない？　何も宣言してないんだから無くて当然でしょう。そしてそれで何も困ることはない。

　もう一つの悪影響は、「物理量が実数値である」という思い込みを強めてしまう点です。

　というのも、例えば量子測定では、測定値集合は別に実数に限られてなんかいないし、任意の可測または位相空間が認められます。 これはごく当然のことで、例えば物理量の測定をするときに、僕らは測定器のUIの状態を見るわけじゃないですか。 それは実数ですか？　なわけ無いですよね？　アナログメーターの針や、デジタル表示器のレジスタ状態をモデル化した某かを 僕らは認識しているわけで、そこまで含めたら測定値集合が実数でなくてはならないなんてことには全くならない。 このメーター系のモデルは、とりあえず確率論の文脈に置くので、可測空間でありさえすればよいのです。 ではどうして古典力学含む物理理論で、大量の実数由来の数学的構造が使われているのか、というのは 単にそれぞれの状況で実数が便利な構造であった、というだけに過ぎません。 なぜなら、個々の理論では実数を使う「動機」がそれぞれ微妙に異なるからです。

　量子力学の測定概念が一気に位相空間や可測空間に一般化できた理由は、 それだけ量子力学が古典力学と違って、内部に複雑な構造を備えていない、非常に素朴な理論であることによります。 古典理論のように、個々の系に複雑な構造が入ってしまえば、その系に対する操作はその構造を保つようなインセンティブが働きます。 ところが量子力学は一般論としてはヒルベルト空間を使う以上のことは言っていませんから、その写像もかなり自由に選べます。 量子力学の古典的対応物は、\bf{Top},\bf{Meas}とかの類であって、間違っても\bf{Symp}とかではないのです。 その意味では、量子力学の公理で「物理量を作用素で表す」も本当はおかしいんですよ。最初からPOVMで宣言するのが筋ってもんです。

2.非有界作用素はいつ必要になるのか？

　半分位続きですが、量子力学の数学的にまっとうな処理というのをやろうとすると、関数解析になるのですが、 そこで面倒くさいのが、非有界作用素の扱いです。というのも、正準量子化とかいうクソ論法に量子力学の当初の仕事が頼ってしまったため、数学的定式化の後で、この位置と運動量に相当する掛け算作用素と微分作用素をまともに扱うハメになってしまったのです。

　非有界作用素の面倒臭さは何かというと、基本的に定義域が全域ではありません。それでも稠密に定義されるものを扱うので、 「ほぼ全域定義」ではありますが、この「定義域」情報を持ち回す必要性によって、 折角作用素「環」構造を作ってあげたのに、例えば加法や結合が、定義域に対してどういう影響を与えるかがまったく非自明で、 個々の要素にいちいち付き合ってやらないといけなくなります。

　ところでですが、量子力学の測定理論概念でのCPTPとかPOVMとかの話は基本的に可分であれば有界作用素の議論で完結します。 これはCPTP概念がもともと作用素環(したがって有界作用素環)に由来したり、測定理論としてのメソッドを確率分布の獲得としてきちんと定めたために、スペクトルが確率値で有界にバウンドされるおかげです。 となると、（有限自由度）量子力学それ自体の定式化では、非有界作用素の登場する所はないのです。

　それで気になるのは、僕らは「いつ非有界作用素との付き合いを余儀なくされるのか」ということです。ごく原始的な測定にはいりません。位置と運動量については、正準量子化を採用しなければよいのです。 たとえば最初からL^2(\mathbb{R})上の左正則表現をとれば、Stone定理でユニタリ表現を分解できるので、 実質運動量に相当するPVMとそのユニタリ作用の概念をもったまま、難なく議論ができます。PVMですから当然有界です。 ユニタリ表現をちゃんと自覚的に召喚すれば、ユニタリなのですから非有界性はどこにも出てきません。 つまり「物理量を作用素で表す」という呪縛を解除すれば良いという話です。そのスペクトルに「物理量の値」としての意味しかないのならば、 それをわざわざPVM要素にかけて積分してヒルベルト空間にねじ込む理由がありません。最初からPVMで扱えば有界になるし便利。 もし、そのスペクトルに変換群が作用しているとしても、PVMの底集合に群が作用していて、 それが密度行列に対するユニタリ表現との間に繋絡自然性条件が走っているとみなせば良いのですから、群作用も問題ない。

　有限自由度の個々の系に関して言う分には、非有界作用素を別の数学で殴る代用手続きがあるように見えます。

　そこで、複数の系の相互作用なんかを考えてみます。たとえば測定のモデルとしてvNプロトコルというのがあり、 それは次の形をしています。

\exp(itA\otimes P)

　ここでAは測りたい物理量でPはメーター系の変換生成子です。しかし、これも取扱自体は有界作用素の範疇で実行できます。 というのもAをスペクトル分解して、これによる合成系のPVM上でPによるユニタリ変換を直積分すれば良いからです。 ユニタリ変換のPVM積分ですから、有界の範疇です。しかしここにはより興味深いことが起きていて、 ここではAのスペクトルの「値自体」がメーターをどの程度動かすかを決めているのです。 なのでAのスペクトルは「ただの測定値」ではありません。メーター系の変換群としての意味があることになって、 それではこのプロトコルを一般化するとしたらどうなるのか？それを組織化するならどうすればいいか？という疑問が湧きます。

　思いかえせば、古典物理でも「物理量の（各点）積」ってこういう使い方をしていたよな、という気がしますね。 例えば解析力学や古典場などで各点積相互作用項を突っ込むことで両者が両者に従って変換されるのが良い例です。 つまり、いい感じの相互作用やある種の動作を引き起こすために、「積をとってみている」わけです。 より素朴な古典物理の場合は、この相互作用それ自体を物理的イメージに基づいて行っている場合があったわけですが、 （例えば常/偏微分方程式を「発見する」場合のdxなどを用いた投機的計算など：弾性体や曲線の方程式とか） いつしかそうした文脈が忘れ去られて、単なる「積構造」だけが引き継がれるようになったのかもしれません。 量子力学でそうした正当な直観を回復する方法論があるのかについてはまだ謎です。

　脱線しました。非有界作用素に戻ってきますが、唯一これやばいなと思うのがあり、それはフォック空間を作る時のLadderoperatorです。

　自由場の量子化、というか量子化はクソなので、単に多粒子系ですが、相互作用をさしあたって深刻に考えなくていい場合は、とりあえずフォック空間を張る事ができます。これは一種の自由テンソル代数のようなものですが、 量子論でのフォックは対称化や反対称化を行ったり、内積も適切に決めてやる必要があるので、 単なるテンソル代数とは微妙に異なります。

　どういう普遍性で定義するのがベストか不明ですが、とりあえずgraded monoidかな？位に思っています。しかしここに問題点があり、粒子を合流させる積演算、およびそこから造られるLadderoperatorは非有界なのです。統計性処理のために。これは量子的調和振動子の計算ともあいます。

　ｳｵｰここへ来て非有界になってしまった。しかしこれはある意味では自然という見解があります。というのも、例えば素粒子現象のように初っ端から多粒子で、かつ識別不能な場合、可観測量とはなにかというと、一粒子の場合はPOVM要素で成立確率を返す汎関数ですが、 このPOVM要素をLadderoperatorでフォック空間に輸送すると、「POVM要素を満たす粒子数期待値」を返す汎関数になるんですよ。 でもこれは確かに自然な物理量に思えます。だって識別不能なんですから、どれがどの事象を成立させるかわからないわけで。

　すると、こうした状況では、単純な確率論としてのメソッドに基づく定式化がまずい気がしてきます。 確率論は汎関数の評価値として[0,1]値だけを相手にすればいいので、有界になりますが、 粒子数期待値となれば[0,\infty)ですから、どんなつまらない物理量でも対応作用素が非有界になってしまいます。どうすれば…

3.STモナド

　Haskellは、他の言語では副作用とかよんでる振る舞いをきちんと型レベルで捕捉することに成功していますが、 そのためにモナドを振り回す必要があります。まぁそれはよいのですが、 例えばIOモナドはほぼなんでもできますが、純粋な計算をしたいというのに、ちょっとIOの力を借りただけで、 IOに汚染されたままになってしまってはたまりません。

　良くも悪くも、型の表現力と統制力が強力なので、やりたいことに対して丁度よい型による表現を探す事が求められているのだと思います。 　そこで破壊的代入や参照や配列更新等ができつつも、最終的に値を純粋に取り出してモナド文脈から戻ってくることの出来るモナドとして STモナドがあります。しかしこのSTモナドの実行関数runSTの型がくせ者で、一見型を見ただけでは、 これが何を意味するのか、これによってどんな利用制限がかかってくるのか、それは何故なのかがピンときません。

runST::forall a.(forall s. (ST s a))-> a

この全称量化こそがSTモナドのキモだったのですが、ようやくそれを了解したのでこれを書いています。

　ところでですが、述語論理において次の証明規則があります。

\forall x. \phi \Rightarrow \phi(t/x)

　これは全称量化の除去規則というやつで、全称量化束縛された変数の具体化に相当します。 このときtは「実質的には」なんでもよいのですが、あくまで推論規則としてこれを見るにはちゃんと制限があります。 それはtは\phiに代入されたときに、t中の自由変数が捕獲されてはいけないということです。 「実質的には」なんでもよい、といったのは、論理命題としてなら、 \phi中の束縛変数をアルファ変換などで置き換えても同値になるためです。 しかし推論規則としてはこの制限は無視できません。今それぞれの論理式はただの記号列だからです。 例として

\phi(-)= \forall y.\exists z. (-) + z > 100 + y

などを考えて、t=-zなどとすれば破綻をきたす事がわかります。

　話を戻しますが、型システムと論理がいい感じに対応してそうというお話があります。

カリー＝ハワード同型対応 - Wikipedia

　詳しくは理解していませんが、型システムがどういう振る舞いをするかのアナロジーを論理に求めることはできそうです。 そこでrunSTですが、何らかの具体的な値を吐かせるために使うわけですから、型変数のaはいずれ具体化されるはずです。 このとき、先の述語論理のアナロジーで考えれば、aの具体化においてsを含むと、これが捕獲される事がわかります。 したがって、runSTを含んで型検査をするときに、aにsを含む具体化を要求するようなコードは弾かれることになります。

　例えば不正なコードとして、

Haskell/存在量化された型 - Wikibooks

の例を見てみましょう。

v = runST (newSTRef True)

が不正ですが、これはnewSTRefの型が

newSTRef::a' -> ST s (STRef s a')

であることによります。このvの型を導出しようとすると何が起きるか見てみましょう。 ST s (STRef s a')をrunSTに代入するのですから、最終的に具体的なaを導出するには ST s (STRef s a')からrunSTの具体化の前提：forall s.(ST s a)を導く必要があります。 このときaは全称量化されていたのですから、sを含んではいけません。 ここで、forall導入を行ってforall s.ST s (STRef s a')としてもa=(STRef s a')となり、 sに依存したaしか示すことができません。そこでこの型チェックは失敗します。

　証明論的なこの不正の理由は納得できましたが、そもそもこのコードはなぜ弾かれるべきなのでしょうか？

　ここで、あえて型ST s aを「環境sと相互作用する返り値型aの計算」だと解釈してみましょう。 newSTRefの型a' -> ST s (STRef s a')は、参照型について「その参照が意味を持つ環境」sがSTRef s a'として 型に組み込まれている事がわかります。 すると、先のコードについては、「環境s上でしか意味を持たない参照」をs以外に持ち出すことが不正であると考えられます。

newSTRefがa->ST s (STRef s a)の返り値は、型変数sが二度出現し、それは同一です。これは

  • 環境s上のアクションであること

  • 得られる参照値は環境sにおいて有効なこと

  • この２つの環境は同一なこと

を示していると考えられます。 　このほかのST文脈を利用する関数も、「ST sの外に出すべきでない」場合は その返り値がsに依存するようになっています。逆に言えばs依存していなければ、外に持ち出す事ができる事になります。

　たとえばSTArrayならfreezeすることによって、immutableArrayになり、これはST sのような文脈を持たないので、 そのまま外に出すことができます。ただし、STArrayをfreezeする動作は配列のコピーを含むので 効率の観点からコピーを省略してそのまま凍結する為の専用関数runSTArrayがあります。 この型は

runSTArray::forall s.ST s (STArray s i e) -> Array i e　

であり、runSTと比べると、あえてSTArray sと、ST sのsが揃えてあります。 すなわち、この配列自体が存在する環境と、それを操作する環境が揃っており、かつ配列の中身には環境sに依存がないことを量化子で強いているのです。

　たとえばこの配列に環境sに依存したインデックスiや要素eが使われていれば弾かれますが、 この配列自体がsに存在することはちょうどぴったり許されるのです。こうすることで、 環境情報について整合的な、環境情報に依存しない要素からなる、環境情報をもつ配列を、 環境情報を持たない純粋な配列として取り出すことが、ぴったり実現できます。

実際にはこのsというのは、実体がありません。実際STのドキュメントを見ると、

Control.Monad.ST

The strict state-transformer monad. A computation of type ST s a transforms an internal state indexed by s, and returns a value of type a. The s parameter is either an uninstantiated type variable (inside invocations of runST), or RealWorld (inside invocations of stToIO).

とあり、RealWorldへ具体化して実質的にIOとなるか、具体化されないままrunSTされるかしかありません。 しかし実体の無いまま全称量化される仮想的な型変数をSTに組み込むことで、 「計算環境」のような文脈と、それに伴う制御を与えていることになります。