インボイス制度問題についての覚書
何が起きているか
まず議論の余地のない側面について:
課税事業者は、消費者等との商取引の売上のうち、10%を消費税として支払う。 その一方で、彼らは仕入れや経費においても課税事業者から税込みで購入している場合が多いため、 二重課税を避けるために、経費や仕入れの課税分は差し引きした上で、残りの部分、 ざっくり言って該当事業者の事業による付加価値分の課税額を収める事になっている。
これを仕入額控除という。
一方、免税事業者はこのような義務は課されていないので、納税義務も、仕入額控除も発生しない。
インボイス制度は、形式的には、こうした商取引の請求書に、その適用税率や税額などを記載するフォーマットを定め、 それによって仕入額控除を行うという手続きを強制するものである。この請求書自体がインボイスと呼ばれる。
したがって、制度が導入されると、インボイス以外の請求書や明細による仕入額控除ができなくなる。
仕入額控除計算のためにインボイスを使うのだから、 課税事業者がインボイスを受け取ることを強制する(インボイスを持っていなければその額の控除をできなくする)のは妥当である。 ところが本制度は「インボイスの"発行"が課税事業者しかできない」という設計になっている。 これが本件の(最大の)問題点である。
インボイス導入前であればこのような制限は無いので、免税事業者への発注に際して支払った金額についても、発注側は控除に利用することができた。 このときはインボイスとは限らない適当な明細や請求書を用いる。
この場合の課税仕入れとは、事業のために他の者から商品などの棚卸資産の仕入れのほか、機械や建物等の事業用資産の購入または賃借、原材料や事務用品の購入、運送等のサ-ビスの購入などをいい、その課税仕入れに係る相手方が課税事業者であることを要件としていません。
免税事業者はそもそも税金を納付しない一方で、免税事業者からの仕入額控除は可能なのは不思議に見えるが、課税事業者の課税はその付加価値に課されているという原則を考えれば自然な状態である(免税事業者からの仕入額控除できなければ、「付加価値に課税」した場合より課税事業者の税が重くなってしまう)。しかし、インボイス制度が実施されると、これが不可能になる。
具体的に見よう。免税事業者が課税事業者から受注した場合(課税事業者のほうが大手であるので、このシチュエーションは一般的と考えられる)を考える。免税事業者は課税事業者に向けて請求書を発行する。
しかし、制度上この請求書はインボイスではない。つまり、発注側課税事業者は、免税事業者からの仕入れを行った場合、その仕入額控除ができなくなる。したがって、発注した課税事業者は、その仕入額×税率分損をすることになるので、そもそもの発注価格を下げようとするか、免税事業者ではなく課税事業者に発注しようとする動機が発生する。大きくわけて3パターンのもっとも極端な可能性がある。
発注側の値下げ要求を全面的に受け入れた場合、受注免税事業者は、おおよそ発注事業者の控除額の課税額分売上が減少する。これはつまり、免税事業者でありながらも事実上の免税事業者ではなくなってしまうことを意味する。しかも免税事業者は仕入れ額控除も行っていない(そもそも納税義務がないので)から、そのままでは二重課税状態となり、最も損をする。
発注側がインボイスによる仕入額控除ができるように、免税事業者が課税事業者に転換した場合、当然消費税を収める必要が出てくるため、免税事業者という立場を手放すこととなり、やはり収入は減る。
価格に転嫁せず、免税事業者が割引を拒否する場合、発注側課税事業者がこれまで通りの価格で発注するにも関わらず仕入額控除を使えないこととなり、(受注側の売上は変わらないのに)発注側は発注額の課税額だけ損をする。あるいはそもそもの取引機会を失う。
現実には交渉によってこれらのケースの中間が起きることになるが、いずれにせよ、免税事業者との商取引に対する暗黙の増税となる。
逆に、課税事業者が免税事業者から受注した場合には、インボイスが発行されるものの、免税事業者はそもそも免税されているからこのインボイスは控除の役には立たず、なにも関係が無い。
同様に免税所業者同士や課税事業者同士でもやはり変化はない。前者はこれまでもこれからもインボイスを発行できないし非課税だから控除もしない。後者はインボイスという新フォーマットに移行する必要はあるものの、それを除けばこれまで通り課税されていて控除も使える。
自分の見解
主張
免税事業者も少ない負担でインボイスを発行できるように整備するか、そもそもの消費税を減税すべきである。
詳細
インボイス制度の目的として、おそらく次の2つが挙げられる。
- フォーマットを固定することによる消費税額の計算や把握の円滑化
- 益税 の撤廃
前者については特に議論する点はない。請求書に限らず、商習慣を合理的に規格化し、円滑化することは基本的に良いことである。 一方、後者の益税について、これが存在するのか存在しないかという議論がある。 この両方に触れておく。
益税は存在しない説
まず益税がどのような定義なのか、軽くググってみよう。
消費者が支払った消費税が国や地方自治体に納められず、事業者の手元に合法的に残ること。中小事業者に対する特例として、売上高5000万円以下の事業者の納税事務負担を軽くする「簡易課税制度」や、課税売上高が1000万円以下の事業者の消費税を免除する「事業者免税点制度」で、益税が発生する。
益税とは、国庫に納入する物として事業者が消費者や顧客から預かった税を、納入せず事業者の利益としたもの。
つまり、消費者(発注者)から預かった消費税を納入していない状態を指している。
この益税概念は字義通り読むと少し奇妙なことになる。
まず、消費税の課税対象は、あくまで金銭を得た受注側の事業者である。
消費税の課税対象は、国内において事業者が事業として対価を得て行う資産の譲渡等および外国貨物の引取り(輸入取引)です(注)。
これは消費税があくまで売上に課されていることとも整合する。どういうことかというと、 受注側が消費者や発注側に価格を提示し、それを支払って取引が成立したとして、 そのことは「その金額の1/11を事業者が納税することに合意した」ことを 意味しない ということである。
たびたび引用される判決は、例えば以下。
「…消費者が事業者に対して支払う消費税分はあくまで商品や役務の提供に対する対価の一部としての性格しか有しないから、事業者が、当該消費税分につき過不足なく国庫に納付する義務を、消費者との関係で負うものではない」
判決確定「消費税は対価の一部」――「預り金」でも「預り金的」でもない|全商連[全国商工新聞]
言い換えれば、消費税という概念が発生するのはあくまで売上に対してであって、消費者や発注者の支払いではない。 仮に購入した商品の値札に消費税の内訳が書かれていたとしても、それを買って支払った段階では、消費税は発生していない。 発生していないのだから(どれだけ消費者が消費税を支払ったつもりでいようとも)、事業者の売上は、消費税の預かり金ではありえない。
つまり 「消費税の預り金」というのは自己矛盾した用語 である。
また、そもそも益税が問題になっているのは免税事業者についてであるが、言うまでもなく免税事業者なのだから、 彼が消費税を納付しないのは定義上当然のことである。したがって 「免税事業者の益税」というのもまた矛盾した用語 であり、 そもそも免税事業者相手の商取引(免税事業者が金銭を受け取る場合)において、いかなる消費税概念も発生しない。
こうした事情のため、益税の法的・会計上の地位は実は曖昧である。支払った金銭に課税されるのは売上としてであり、免税事業者ならそもそも課税もされない。 仮に小売店の値札に110円(税込み:税10円)のように書かれていたとしても、結局店の売上は110円であり、それ以上でもそれ以下でもない。 このような表示を見た時に「私こと消費者が支払い額から10円の消費税を納付するように販売店に確約した」と思いこむのは自意識過剰なのである。 結局益税という概念は消費納税のプロセスにおいてどこにも出現しないのだ。
益税は存在する説
では、益税という概念には全く実体がないのか?というと、もちろんそういうわけではない。これは至極簡単な話である。
仮に、全く同じ事業/仕入れ/売上を行っている2つの事業者があり、一方は課税事業者、もう一方は免税事業者だとしよう。 この2つの事業者は消費税について次のように振る舞う。簡単のため税率を10%に統一して考える。
売上をX、仕入額をYとしたら、課税事業者は10/11(X-Y)の利益となり、免税事業者はX-Yがそのまま利益となる。 したがって、全く同じ条件で免税事業者と課税事業者を比較すれば、免税事業者のほうが1/11だけ有利である。 これは当然のことであり、もしこうなっていなければ免税事業者という名前自体がふさわしくないだろう。
"益税"をどう解釈するべきか?
益税が存在するという説は、要するに 免税事業者は免税されている分収入面で有利であるという自明な主張 に過ぎない。 そして益税がこの意味でしかないなら、もちろん益税は(免税事業者という区分が存在する以上)存在する。 そしてまさしくインボイス制度は免税事業者の立場を間接的に破壊することによって益税を抑制するだろう。 何も難しいことはなく、益税を敵視するというのは、免税事業者の"免税特権"を敵視することそのものである。
しかし、この益税概念を どのように受け止めて解すべきかについては、免税存在しない説をきちんと踏まえる必要がある。
というのも、益税に対する敵意には、この点を不当に解釈したものが度々見られるからだ。
すでに述べたように、免税事業者への発注ないし免税事業者からの購入および金銭支払の段階では、消費税は発生していないし、消費税支払いの確約もしていない。
もしそのように思えるのだとしたら、それは消費者/発注者が勘違いしているか、騙されているだけである。消費者はその名に反して、免税事業者にも課税事業者にも、一円たりとも消費税を支払ってなどいない。事業者は単に、自身が払う(または払わない)であろう消費税を見越して、適当な販売価格をオファーしているだけで、それは全額が対価である。
課税事業者が免税事業者に発注した場合に、仕入額控除として発注額の課税額を計算するとしても、課税事業者に適切な税を課すための計算に過ぎず、「免税事業者がここで計算された仕入額控除税額を納付している」ことを意味しない。
したがって、「発注者や消費者が支払った消費税を収めていないのだから、益税は不当であり撤廃すべきだ」というのは単に間違っている。
「我々消費者や発注者が、免税事業者に消費税を払った」ことなど一度もないのである。
こうした言い方は、払ってもいない税を着服しているという冤罪をかけている。
免税事業者が消費税を納めないのは、ズルをしているのではなく、最初から免税を前提とした価格をオファーしているのだ。 免税を前提とした場合のほうが課税を前提とした場合よりも、余計な出費がない分、高品位な仕入れや人件費に回すことができるのだから、発注者・消費者は免税事業者とともに、すでにその恩恵に預かっているのである。 決して免税事業者だけが免税という恩恵を独占しているわけではない。仮にそう思えないとしても、もし免税事業者が業態をそのままに課税事業者に転換したならばこの恩恵は失われ、双方が損をするのだから、それはあなたが気づいていないだけである。
その一方で、免税事業者が、請求内訳として消費税を記しているにもかからわず、実際には税が発生しないというのが混乱を招いているという意見はあり得る。 つまり、免税事業者が「x円で売ります」「このうちy円は消費税です」とオファーしてきた場合、消費税が自分に課されていると思いこんでいる哀れな消費者が騙されてしまい、総額を多少高いと思っていても支払ってしまうかもしれない。 免税事業者が消費税が発生するかのような請求を行うことがあるのは何故か、そしてそれは道義的にどうなのかという点については別の側面から検討が必要だろう。
例えば、
免税事業者は、取引に課される消費税がありませんので、「税抜価格」を表示して別途消費税相当額を受け取るといったことは消費税の仕組み上予定されていません。 したがって、免税事業者における価格表示は、消費税の「総額表示義務」の対象とされていませんが、仕入れに係る消費税相当額を織り込んだ消費者の支払うべき価格を表示することが適正な表示です。
つまり、免税事業者は仕入額控除ができないため、完全な意味での免税状態にはなく、これを価格に転嫁しておくというのはひとつのロジックとして成り立つ。 ただし通常仕入額 < 売上額になるはずなので、このロジックでは仕入額の割合を超える分の消費税を正当化できるわけではない。
いずれにせよ、免税事業者にとっては税込/税抜価格という区分自体が意味をもたない。
益税概念はサルベージ可能か?
益税を「発注者や消費者から受け取った消費税を留保したもの」と解釈することは間違っていると述べた。 では益税をどのように理解するのが適切なのか? おそらく益税という名称に込められた本来的な意味は、「免税事業者が免税されていることによる利益」 だと思われる。 では、 この意味での益税を、具体的な数値として計算することはできるだろうか? つまり、免税事業者の収支の情報から、 「この事業者は課税されている場合よりもx円得している」という値を算出することができるだろうか?
先の益税概念の説明では、全く同じ事業を実行する免税事業者と課税事業者を比較した。その結果、免税事業者は課税事業者よりも利益の面で1/11有利となった。 これはつまり、「免税事業者は、たとえ課税されていたとしても、全く同じ事業を行う」と仮定しているに等しい。 これはどう考えても非現実的な仮定である。 なぜなら、事業者は事業者自身に課されている課税計算方式に鋭敏に反応するはずで、 課税されているとわかっているならそれを前提とした事業計画を立てるはずだからである。
そうなると、ある期間における免税事業者の収支から、「課税されていた場合の収支」を計算しようとしても、 推定以外にはやりようがない。例えば、事業者の行動性向をモデル化し、効用関数を推定し、課税した場合の振る舞いを予測し....と言った具合だ。 これは現実的精度で実行するのは到底不可能であるし、会計計算をこのような不確実なやり方で実行したらメチャクチャになってしまう。
会計計算上は、益税というのは計算しようがない。 これが「益税が存在しない」ということの本当の意味である。
免税事業者は課税死荷重を回避できているから、免税事業者とのやり取りでは、 事業者および消費者共に利益を得ている。ここまでは均衡の一般論として結論できるし、だれも否定してはいない。
だが、具体的に免税事業者がこうした死荷重回避によっていくら得したか、そして消費者・発注者 も いくら得したかは、 現実に観測可能な数値からは計算しようがない。だから会計上は益税という値は出てこないのだ。 現実の数値からは計算も決定もできないのだから、存在しないもとのして扱いざるを得ないのである。
原理的に計算も決定もできない以上、「免税事業者はy円得している」という言説はすべて不正確な推定に過ぎないといえる。
そしてこれが厄介な現象をもたらす。つまり、政治的立場として益税を敵視する人間は、免税事業者の行動性向について、都合の良い仮定をおき、この値を可能な限り大きく見積もることで、課税死荷重回避による利得を事業者が独占していると解釈したがるだろう。 これがまさに「免税事業者は消費者が払った消費税を着服している」という誤解において起きていることなのだ。
こうした「益税」の過大評価からくる批判は、そっくりそのまま彼らに返ってくる。というのも、以下に述べるように、課税は本来事業者と消費者の双方に損失を強いるものであり、免税とはその裏返しで、双方が利益を得ているからである。消費者側の「益税」を無視し、事業者側の「益税」だけを敵視し、それが撤廃されたことによって消費者も損をするからだ。
免税事業者と課税事業者の公平性を議論したいのなら、益税概念はあくまで「免税事業者は免税されている」以上でも以下でもない ことを理解する必要がある。
課税による損失について
免税事業者が免税される状態が撤廃され、事実上課税状態になるとどうなるかについては、典型的な経済学のトピックとしてあるように、 供給曲線の上シフトによって、いわゆる過剰負担/死荷重が発生する。つまり、課税は事業者と発注者の双方に損失を強いる。
もちろん、課税事業者との取引についてはインボイス以前からもこの損失は発生していたわけであり、 そこに小規模故に死荷重を逃れていた免税事業者が更に仲間入りするということである。
これは一見公平になるように見えるが、そもそも免税事業者が実質課税事業者に転換したところで 誰も得をしていない。 免税事業者は収益が上がりにくくなり、発注側は免税事業者への発注コストが上がるだけである。 「免税事業者はズルい。彼も等しく課税されるべきだ」というのは心情的には理解できるが、その結果として引き起こされる状況は誰の得にもならない。 免税事業者と課税事業者の扱いの違いが何らかの歪みをもたらしている可能性はあるが、 免税事業者はそもそも規模が限定されており、一方的に収益を増やすこと自体が不可能であるからこれも限定的だろう。
免税事業者が課税転換して消費税を収めるようになることで税収増を期待するかもしれない(算出方法にもよるが千億ほどと推定されている)。しかし政府支出は予算制約を持たず本来的に裁量的なものであり、税収とは全く独立である。 免税事業者とその取引事業者が税を負担して国庫に収めたところで、政府が補填となる財政政策を実行してくれる保証もなければ、そもそも政府がその気になれば税収なしでも財政政策は実行できる。従って特定の税収と特税の財政政策の間には何の因果関係もない。免税事業者への実質課税で徴収した税収が何かに役立つと考えるべきではない。それは何の役にも立たない。
免税事業者の"益税"が気になるならばこそ、課税事業者の死荷重をまず気にすべきである。 というのも、"益税"というのは、結局課税事業者の死荷重の裏返しに過ぎないからだ。 「免税事業者が免税されていることによる利益」は「課税事業者が課税されていることによる損失」と全く同じはずである。 課税事業者との商取引では、課税事業者は当然売上から支払うであろう消費税を見越して価格をオファーするはずであり、 価格は上がるし利益は減る。免税事業者はこれを回避しているので、消費者にとっては安く、免税事業者にとっては高く売買できていた。 従って、この不公平を気にするならば、より抜本的な解決として消費減税が挙げられる。
"益税"問題 < 各事業者の収入
ここで一旦免税事業者という地位について一応検討しておこう。 免税事業者が課税事業者よりも有利な状況にあるのはもちろん事実である。 しかし、これはあくまで両者が全く同じ規模と条件で行っていた場合の話であり、 当然ながら免税事業者には売上1000万以下などの条件がついている。
小規模な課税事業者は少ないだろうし、大規模は免税事業者は存在しないのだから、 全く同じ規模と業態の、免税・課税事業者を単純比較するというのはあまり現実的ではない。 大規模な事業になれば、その分効率的な生産も可能になるだろうが、小規模ではそうもいかない。 したがって、線形な比較によって免税事業者が有利であると結論づけることにも疑念が生じる。
1000万以下の弱小事業者が、(全く同じ事業を行った時に)利益計算の点で1/11有利な地位にいることをどれだけ「不当」と捉えるかは、 各位の価値観によるところもあるだろうが、上記の事情から、自分は特段不当だとも思わない。 従って、現状の免税事業者の"益税"とやらを積極的に潰す必要も感じない。
よって、自分の意見としては、インボイス導入を見送るか、どうしてもインボイスを導入するというのならば、 免税事業者も容易にインボイスを発行できるようにするなどし、いわば"益税"を維持してもよいと考える。
しかしここに加えて 抜本的な解決として消費減税を実行してもよい。というか、それが最も望ましい。 その場合は"益税"も、 課税事業者側が免税事業者側に近づくことによって相対的には圧縮され、インボイス云々などの実質的意味も薄れるが、 いずれにせよ免税事業者およびそれらと取引する関連事業者の収入は守られるからである。
これは益税概念にばかり執着している人間からすると不可思議かもしれないが、 そもそもインボイス反対も、消費減税も、各事業者の収入減を憂慮してのことなのだ。
言ってしまえば、免税事業者と課税事業者の線形・相対的な公平性("益税")をどちらに寄せるかについてはこの際些末な問題 なのである。 実質的な増税を阻止することで、 各事業者の収入を絶対値として下げないことのほうが遥かに重要である。
インボイス反対と減税はどちらも各事業者の絶対的な収入を守るという目的で同じ方向を向いている。 だから大幅な消費減税によって"益税"が吹き飛んでしまうなら、それはそれで全く構わないのだ。 そのときはインボイスに反対する理由もない。消費税を無視できるほどになればインボイスの有無自体どうでも良くなる。 減税により課税事業者の負担は減り、免税事業者は何の変化もないか、仕入額が少し安くなるかもしれない。 何れにせよ、彼らの収入は守られる。
免税特権という"益税"に気を取られている人は、まずそもそも本件が実質増税である点、および現在の経済情勢にそぐわない消費税率についての是非を表明すべきだろう。 また、免税事業者が課税されたところであなたの収入は一円も増えず、もし取引があるならコストアップによる痛み分けにしかならないが、 そうして実現される「公平な重税」は果たしてそれに勝るすばらしい状態なのかもよく考えるべきだ。
本当に望ましいのは「公平な軽税」ではなかったか? あるいはそれがすぐに実現しないとしても、「公平な重税」は「不公正な重税と軽税」よりも望ましいのか?
消費税に限らずすべての税は貨幣の破壊である。したがって、 免税事業者を課税転換させることは、彼らが多めに取っていた貨幣を消費者側(?)に取り返すことではない。 消費者と事業者が、売買のたびにお互いの貨幣を少しずつ捨てることに合意することである。
例えば詐欺・詐取や賃金未払いなどは、いずれも抑制すべき悪行である。だがそうした犯罪行為によって、 加害者は利益を得て、被害者は同じ損失を出しているという意味では、何らかの価値が消滅したわけではない。 しかし免税セクションを課税転換するということは、これとは全く違う。 憎き免税事業者を吊し上げ、勇ましく課税転換させることによって、免税事業者と我々の両方に損失を出すのである。 ああ、なんという素晴らしい公平さだ。
インボイスを発行できる適格請求書発行事業者の個人情報が公開されてしまっているという問題については 当然改善したほうがいいと思うがここでは詳しく触れない。
増税回避/減税という本命
自分は自営業者ではないし、正直免税事業者の地位と公平性にそこまで関心がない。 免税事業者が免税されているという「不公平」な状況もそこまで不当とも思えないが、 免税事業者の優遇をどの程度まで実施しておくべきかという点については、 あったっていいだろう、位の立場であり、具体的に適切な優遇の水準がどのくらいかについては確たる意見はない。
益税概念については、そもそも消費税込み/税抜き価格が併記されていることによって、 「消費者が、税額を全部払っている」と勘違いしていることが遠因となっている気がする。 どれだけ魅力的な税抜き価格が提示されていたとしても、 どれだけ消費者がその差額である消費納税の負い目を感じても、 消費者が払うのは結局税込み価格であり、この時点では事業者はこの表示税額を納入する義務を消費者に対して負ったりなどしない。
各事業者は自身の売上に課されるか課されないかする税額を見込んだ上で、(税込み)価格を決定してオファーしているだけだから、 同じ条件では課税事業者に比べて免税事業者のほうが、消費者も事業者も得をする。 しかし一部の人間は益税への嫉妬のあまりか、「平等な課税」によって等しく貧しくなること を望んでいるかのようだ。
そしてこれこそが本件に反対すべき本来の理由である。
現行のインボイスに反対する側にいる理由は、シンプルに実質的な増税だからだ。 この増税が弱小免税事業者を狙い撃ちにしているという点でもよろしくない。
ここで、税収を維持しなければならないという思い込みによって、 減税や益税を他の部門に転嫁していると勝手にみなす藁人形論法は不当であることは予め釘を指しておく。
税の目的は税収を上げることではない。貨幣価値の担保という基幹機能を除けば、 格差の解消や悪行の抑制である。通貨主権を持つ日本で財政収支をバランスさせる必要もないので、 消費税によって国庫を潤す必要もない。現時点で消費増税する必要などまったくなく、 むしろ減税とともに需要を支え、それによって生産を維持拡大しなくてはならない局面にある。
インボイス制度はその制度的欠陥によって、 免税事業者の地位を切り崩すという形で間接的な消費増税となっている点がマズい。現在の経済局面からすれば、 免税事業者の免税という地位が不公平というならば、課税者の減税によってそれを正すべきであり、 免税事業者に実質的な課税を復活させたところで、誰も得をせず、単に収入減(貨幣供給減)によって経済が縮小するだけである。 減税する、または増税を回避することで、各種事業者の収入減を阻止するというのが最優先であり、 免税事業者という地位の公平性はこれに比べれば二の次である。益税などあってもなくてもよい。 そもそも消費税を減らしてしまえばインボイスやら益税やらの問題は相対的にどうでも良くなるのだから。 このため減税とインボイス反対は全く矛盾なく両立するのだ。 積極財政のインボイス反対派が守ろうとしているのは、免税事業者の相対的優位性なんかではなく、絶対的な収入の方である。
以上より、自分の考える限り望ましい政策に順位をつけると次となる。
MMT"以前"としての中銀システム
これは何
MMTと主流派の経済論争が勃って久しいが、色々調べていくうちに、両者の間の対立というのが本当に微妙なもので、正直なんでこんなことで喧嘩していたのかわからないという気持ちになってきた。たとえば、個人的に直近に読んだ
https://www.newsweekjapan.jp/noguchi/2019/07/mmt1.php https://note.com/motidukinoyoru/n/n266cd5b29bf9
などは解像度が高くてどちらも参考になる。ところで、前者(野口旭氏はリフレ派であり、タイトルにあるようにMMTについて若干批判的である)のパート4から引用すると、
誤謬その1:政府は家計と同様な「予算」の制約に直面している。
誤謬その2:財政赤字(黒字)は悪(善)である。
誤謬その3:財政黒字は一国の貯蓄を増加させる。
誤謬その4:政府財政は景気循環を通じて均衡されるべきである。
誤謬その5:財政赤字は、希少な民間貯蓄を奪い合うことになるため、利子率を引き上げ、民間投資をクラウド・アウト(締め出し)する。
誤謬その7:政府の浪費は財源の喪失を意味する。
誤謬その8:政府支出はインフレを生む。
新旧ケインジアンを含む反緊縮正統派はおそらく、これらが「主流派の誤謬」だと言われれば、その誤謬を信じている主流派とはいったい誰のことなのか、よくメディアに出てきては赤字赤字と大騒ぎする緊縮保守派のことだろうか、などといぶかしく思うであろう。
MMT(現代貨幣理論)の批判的検討(4)─クラウド・アウトが起きない世界の秘密|ニューズウィーク日本版 オフィシャルサイト (NewsWeek日本語版 2019/8/8 野口旭「MMT(現代貨幣理論)の批判的検討(4)」)より引用
おわかりだろうか、この内幾つかは、MMTの"通俗的な"宣伝で主張されることであったりするのだが、実のところこれは主流派、つまり通常のマクロ経済学の知見に別に反しないというのだ。
ではなんでMMTは異端などと祭り上げられる(ていた)のか。上記の記事によれば、金融政策についての中銀の能動性や振る舞いについて、リフレ派と MMTerが(共に積極財政に迎合的という意味で政策面では共闘できるにもかかわらず)対立している。また、そもそもの金融政策(金利政策)の有効性についても対立がある。
この両者の微妙な違いに踏み込んでいくのはそれはそれで興味深いのだが、twitterなどの経済談義では、この「MMTvs主流派の本当に微妙な対立点」を議論するレベルのはるか手前の水準の喧嘩が発生したりする。例えば又貸し信用創造やクラウディング・アウトorイン論や根強い財政破綻論だ。相変わらず新聞は財政再建記事を書くのを止めないし、定期的に現れるクニノシャッキンガーが絶滅する兆しもない。おそらくこうした誤解は、現代の金融システムを把握することなく、直観的な商品貨幣観バイアス、民間企業の財務観からまったく離陸できていないことからくるのではないか。
実のところ、上記に引用された誤謬は、現実の金融システムがどのように資金を融通しているかを多少なり落ち着いて記述してしまえば、わりとすんなり解消される。そしてそれはMMT以前においても常識であって、特に議論の余地はない。であれば、まずこの金融システムがどのように決済を行っているかを把握すべきだろう。そういうことで、中央銀行を中心とした金融システムがどのようになっているのかを一通りまとめておくべきと思い、これを書いている(ただし、手続きの順番などの細部は無視している)。つまり、以下に記すかなりの部分は、MMT 以前の 内容のつもりである。これを前提として、ようやくそれぞれの派閥間の対立点の議論や政策の是非、細やかな分析に入っていくことができる。
MMTの寓話としてしばし「モズラーの名詞」が登場する。これは租税貨幣論による貨幣需要の発生を単純化したもので、通貨主権が貨幣需要を毀損することなく貨幣そのものを供給できるという示唆を与える。この寓話の唯一の問題点は、単純すぎることだと思う。 つまり「現実にはそんなふうになってないのではないか」ということだ。確かに、日本では時の政権が日本銀行券を刷って支出しているわけではない。しかし実質的には同じことができ、それは金融政策(中央銀行)と財政政策(政府)の連携によって実現される。そのことを理解するためにも、やはり中央銀行を中心とした金融システムの概要を知っておく必要がある。
中銀システム
不換通貨を発行する中銀と政府による分離した金融/財政体制を備えた国があり、各国の預金者および金融機関が、口座をもつことによって接続されている状況を考える。日米英など、通貨主権をもち、政府と分離した中央銀行とそこに準備預金を備える金融機関によって金融および決済システムが構築されている国はこれが当てはまる(当然ユーロ圏は除外される)。図示すると以下になる。呼称がみつからないので、この記事では便宜的に中銀システムと呼ぶことにする。下図はこのような国が2国存在している場合である。
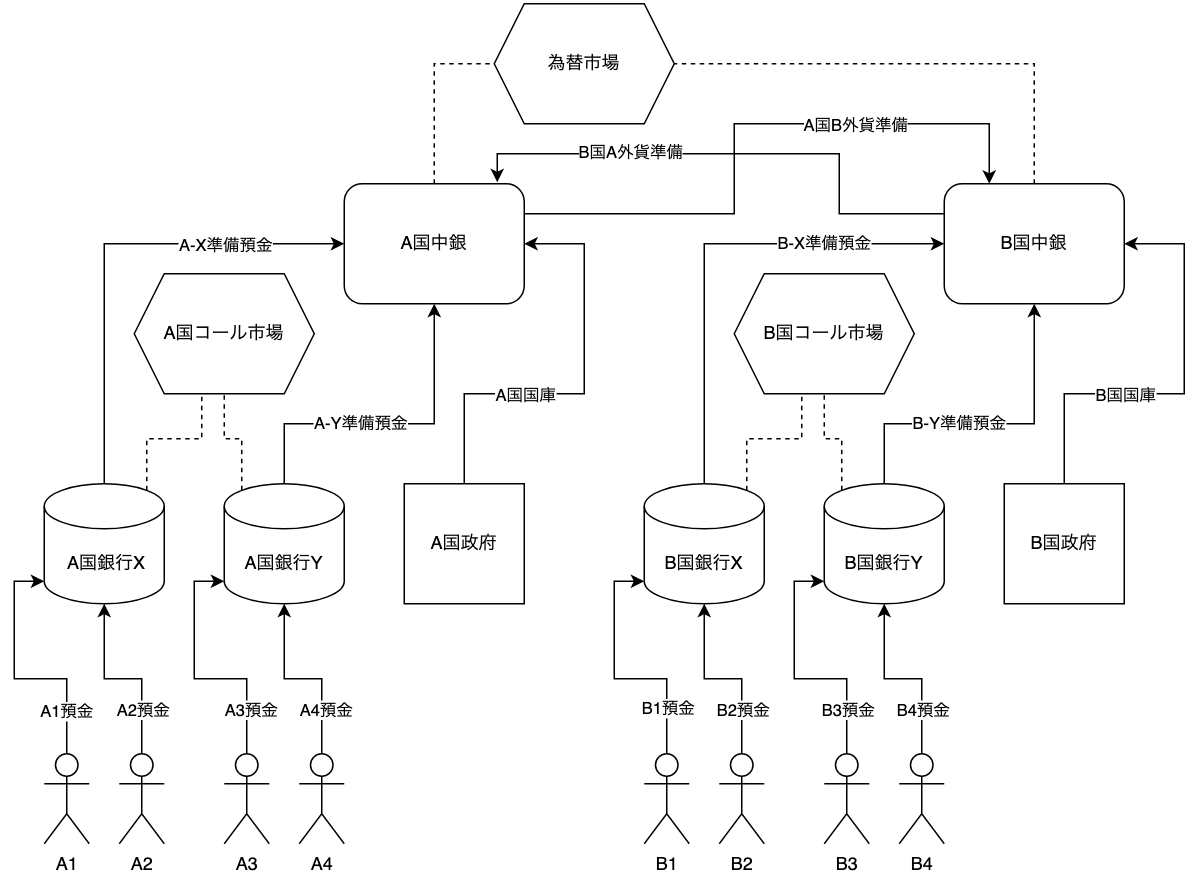
矢印は預金口座を持つことを意味する。 破線は市場に参加していることを意味する。
上図の登場人物が何で、彼らに何ができるかという前提条件をまとめておこう。
- A国銀行は同様にZ,W...と続いてよい。
- B国銀行も同様。
- そもそも国C,D,E...と続いてよい。
- A国民間預金者A5,A6...と続いてよい。これらはA国のどの銀行に口座持ってても良い。
- B国民間預金者も同様。
市中預金者の資産の大半は銀行預金だが、銀行と中銀はこれ以外に国債や投資信託などの金融資産などを持てる。
- ここにいる全員は、預金および適当な金融資産や証券などを持っていてよい。
- 銀行は、即時の出金需要、及び両替用に外貨の現物や現金を持っていてよいが、その量は相対的に少ない。
- 預金者も、日常決済のために現金を持っていてよいが、その量は相対的に少ない。
各銀行は信用創造によって預金を発生させられる。
- 中銀及び銀行は、その預金者に対して、出金需要(預金債務の履行)に応じられ、該当国の金融規制を満たす限りにおいて、信用創造による預金創出ができる。
- 中銀は預金者である市中銀行に対して、準備預金を支払い手段とした、国債などの金融資産の売買オファーができる。
- 各国の発行紙幣は、中銀の債務証書である。中銀の準備預金はこの現金として出金できる。紙幣印刷権限は中銀に独占されている。
- 中銀の準備預金の債務とは、「要求あり次第、同額の紙幣を払い出す」ことである。したがって、中銀は常に準備預金の債務を履行できる。
- 中銀の発行紙幣の債務とは、「要求あり次第、同額の紙幣を払い出す」ことである。したがって、紙幣を中銀に持ち込むと同額の紙幣が得られ、最初に支払った紙幣の債務は消滅する(新しく発行した紙幣の債務が生まれる)。つまり不換であり、中銀は紙幣をそのまま返すことでこの債務を履行し続けられる。
この他、政府の国庫となる特別な準備預金(中銀の口座だが、通常市中銀行の準備預金とは区別される)や、銀行間の預金融通などのシステムがある。
- 政府は、中銀および市中銀行に対して、準備預金を国庫振替を支払い手段とした、自国通貨建て国債の売却オファーができる。中銀にたいしては、各国財政法がこれを制限しているものの、日本の場合は但し書きにより、国会の承認を得た場合に限り、国債の中銀直接引受が可能である。
- 中銀は、他国の中銀に口座を持つことで、外貨準備を保有する。
- 各国政府は(中銀と政府が分離している場合には)中銀に口座を持つことでこれを国庫とする。もし統合政府モデルで考える場合は、中銀と政府を一体化してもよい。
- コール市場では一時的な準備預金需要に応じるために無担保で金利のみを設定した短期貸し出しが行われる。これをコールレートとよび、現在日本銀行の金融政策目標となっている。具体的には、日銀は、預金者である銀行に対して、国債等の金融資産売買を持ちかけることでこれを制御する。
- 一方準備預金需要に対して中銀が直接特融や貸越を行う場合の金利は公定歩合とよぶ。
- 為替市場では、変動相場制国は、売買オファーがマッチした場合に売買が起きる。固定相場制国の場合はその相場によって売買に応じる必要がある。
預金と準備預金は区別する必要がある。
- マネーベース、ベースマネー、マネタリーベースは、通常準備預金と現金のことを指す。つまり、中銀の債務=実際に発行されている貨幣のことである。ただし、準備預金は銀行業務と国庫の運用に用いられ、通常経済活動には用いられない。
- マネーサプライは、市中銀行預金と現金のことを指す。これは経済活動の決済および貯蓄に直接用いられる貨幣すべてに当たる。銀行員以外の人間が現実に操作する貨幣はすべてこれであり、経済状況による貨幣需要と市中銀行の融資の可否によって増減する。
このような認識のもとで、通常の
が、どのように行われ、それを行った場合に何が起きるか、どのようなインセンティブが働いているか、またどのような市場への影響がありえるか、を考える。
具体的に、これらの操作を記述するにあたって、複式簿記の仕訳に倣った記述を行うのは合理的である。というのも、図に登場するノード間の売買や送金決済を行う場合、この図で預金者関係によって接続されている銀行や金融機関がこれを実行するために、様々な金融資産を操作するからだ。そしてその多くは今や電子的記帳であることが多い。つまり、経由する金融機関は、そのバランスシートに決済に必要な金融資産の増減の仕訳を記帳することで、離れたノード間の決済を実現する。預金関係や市場を通さない、物理的な貨幣引き渡しによる決済手段ももちろん存在するが、それは相対的に少ない。
仕訳は、ある者が
- 何を得て、何を失ったか
または
- どんな債務を負い、どんな債務を解消したか
を左右同額に分けて記していく。以下のルールに従う。
- 左(借方)に得たもの(債権)を記入していく。
- 右(貸方)に負ったもの(債務)を記入していく。
- 借方貸方に同額の金額が書き込まれ、これはかならずペアになっている。
- 資産の減少、債務の解消のように、変化が負数になる場合は、記入欄を逆にして、かならず正の値が記入されるようにする。
- 例えば、借金をした場合、現金(または預金)を得て返済債務を負う。したがって
- 現金(または預金)を左(借方)
- 債務(通常「借入金」と書く)を右(貸方)
- 一方借金を返済した場合、現金(または預金)と債務を同時に失うので、
- 「債務を失った」という意味で得なので左(借方)に、正の値で書く。
- 「返済で現金を失った」という意味で損なので右(貸方)に、正の値で書く。
- 例えば、借金をした場合、現金(または預金)を得て返済債務を負う。したがって
例えばサラ金でお金を借りた場合、
| 借方 | 貸方 |
|---|---|
| 現金100 | 借入金(借入債務)100 |
だが、これを返済した場合は
| 借方 | 貸方 |
|---|---|
| 借入金(借入債務)100 | 現金100 |
とする。つまり、正の財の増加と負の財の減少は、その絶対値を左に、負の財の増加と正の財の減少は、その絶対値を右に記入していく。 これは現金を借りた側だが、貸したサラ金業者の仕訳はこれの逆になっている。 つまり、複式簿記は、ある取引に関係する全員の仕訳を集めると、1次元単体複体の環形式のようにつながって相殺する仕組みになっている(名目勘定が含まれなければ輪っかになる)。
なお以下で用いる勘定項目は標準的な語法ではない(簿記での標準的な語法を調べるのが面倒だった...)
具体的な決済手続き
預入
次のことが起きる。
- 預金者A1は現金を銀行に預け入れ、預金を獲得する。
- A-X銀行は現金を獲得し、預金債務を負う。
A1:
| 借方 | 貸方 |
|---|---|
| 預金100 | 現金100 |
X銀行:
| 借方 | 貸方 |
|---|---|
| 現金100 | 預金100 |
さらに、預け入れ支店の業務用の現金がすでにあるなら、これを中銀に預ける。 次の操作を連結する。
- 銀行は現金を中銀に預け入れ、準備預金を得る。
- 中銀は現金を獲得し、準備預金債務を負う。
X銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 現金100 |
中銀:
| 借方 | 貸方 |
|---|---|
| 現金100 | 準備預金100 |
銀行は準備預金を獲得すると、資金繰りが容易になる。この意味で、預金者が本当に"最初から"現金を持っているなら、その預け入れは銀行の資金繰りを改善する。しかし日頃我々が持っている現金が"最初から"現金であった可能性(割合)は高くない。 なぜなら大抵の場合我々は預金として収入を得、預金のまま貯蓄しており、その一部を出金して使っているが、それは賃金を出した会社への融資から来ている可能性があるからだ。仮にその会社が売上や商取引で現金や預金を受け取ったとしても、やはりそれも誰かへの融資として発生した可能性がある。我々が預金を引出して現金化し、再度預けても、単に預金引出しで減った準備預金が預け入れで元に戻ったというだけである。あなたが現金を持っているとしたら、それはあなたが自身の労働や取引で得た預金について、銀行と中銀が準備預金を切り崩して紙幣をよこしたからであり、あなたが"最初から"その現金を持っていたとは考えにくい。
融資
次のことが起きる。もっとも単純な操作である。
- 預金者は返済債務を負い、預金を手に入れる。
- 銀行は貸付債権を獲得し、預金債務を負う。
預金者A1:
| 借方 | 貸方 |
|---|---|
| 預金100 | 借入金(借入債務)100 |
X銀行:
| 借方 | 貸方 |
|---|---|
| 貸付金(貸付債権)100 | 預金100 |
銀行は、これで発生した預金債務による出金や送金の需要に応じる必要があるが、預金債務の増加に対して、これら業務による準備預金需要の増加はかなり小さいはずである。このため、銀行は預金デフォルトを起こすことなく、準備預金以上の預金債務を抱えられる。
出金
次のことが起きる。
- 預金者は預金を減らし、現金を手に入れる。
- 銀行は預金債務を解消し、現金を失う。
A1:
| 借方 | 貸方 |
|---|---|
| 現金100 | 預金100 |
X銀行:
| 借方 | 貸方 |
|---|---|
| 預金100 | 現金100 |
もし、十分な現金が支店に置かれていない場合、中銀支店からこれを融通する。つまり、次の操作を連結する。(常にこれが行われるとしたほうが単純である)
- 銀行は準備預金を減らし、現金を得る。
- 中銀は準備預金債務を解消し、現金を失う。
X銀行:
| 借方 | 貸方 |
|---|---|
| 現金100 | 準備預金100 |
中銀:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 現金100 |
つまり現金の預け入れの逆である。
送金
同じ銀行にいるA1,A2の間で送金する場合、極めて単純である。銀行Xがそれぞれの預金残高を入力するだけであり、現金を必要としない。
- A1は預金を失い、A2への支払債務を解消する。
- 銀行はA1の預金債務を解消し、A2の預金債務を負う。
- A2は預金を獲得し、A1への請求権を失う。
A1:
| 借方 | 貸方 |
|---|---|
| (支払債務100) | 預金100 |
X銀行:(この行は相殺するためなくても良いが、誰への債務かを区別して一応書いておく)
| 借方 | 貸方 |
|---|---|
| A1預金100 | A2預金100 |
A2:
| 借方 | 貸方 |
|---|---|
| 預金100 | (支払債権100) |
異なる銀行にあるA1,A3の場合、中銀が媒介する。
- 銀行XはA1の預金債務を解消し、準備預金を失う。
- 中銀は銀行Xの預金債務を解消し、銀行Yの預金債務を負う。
- 銀行YはXから振り返られた準備預金を獲得し、A3への預金債務を負う。
A1:
| 借方 | 貸方 |
|---|---|
| (支払債務100) | 預金100 |
X銀行:
| 借方 | 貸方 |
|---|---|
| A1預金100 | 準備預金100 |
中銀:(この行は相殺するためなくても良いが、誰への債務かを区別して一応書いておく)
| 借方 | 貸方 |
|---|---|
| X準備預金100 | Y準備預金100 |
Y銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | A3預金100 |
A3:
| 借方 | 貸方 |
|---|---|
| 預金100 | (支払債権100) |
しかし実際には、準備預金を送金のたびにいちいち操作はせず、逆方向の送金などと相殺してまとめて操作する。
出金および送金時の準備預金調達
出金や送金による準備預金の振替えおよび出金操作において、銀行Xの準備預金が不足した場合、銀行Xはコール市場で準備預金を調達できる。つまり次の操作が追加され、後日これの逆操作が行われる。
- 銀行Xは、準備預金を獲得し、返済債務を負う。
- 中銀は銀行Xの準備預金債務を負い。銀行Yの準備預金債務を解消する。
- 銀行Yは、Xへの貸付債権を得、準備預金を失う。
X銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 借入金(借入債務)100 |
中銀:(この行もなくてよいが、便宜的に書いておく)
| 借方 | 貸方 |
|---|---|
| Y準備預金100 | X準備預金100 |
Y銀行:
| 借方 | 貸方 |
|---|---|
| 貸付金(貸付債権)100 | 準備預金100 |
中銀の直接貸越が認められている場合には、中銀が直接貸付をする場合もある。これも後日逆操作を行う。
- 銀行Xは、準備預金を獲得し、返済債務を負う。
- 中銀は銀行Xの貸付債権を得、銀行Xの準備預金債務を負う。
X銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 借入金(借入債務)100 |
Y銀行:
| 借方 | 貸方 |
|---|---|
| 貸付金(貸付債権)100 | 準備預金100 |
銀行Xは、返済日にコールレートなり公定歩合なりの金利を(もちろん準備預金で)後日支払う必要があり、準備預金の目減りは銀行業務に支障をもたらす可能性があるため、準備預金の枯渇を避けるインセンティブを持つ。一方、準備預金には利息がついていないので、銀行業務に必要な分を超過する準備預金については場合はコール市場での貸し出し、有利子の金融商品の購入、あるいはそもそもの新規融資による債務増加などでギャップを解消しようとする。
この"銀行業務に必要な分" というのは一概には言えないが、準備預金制度のように制度的に一定の水準を強制する場合もある。準備預金率は非常にひくく、1%前後である。準備預金制度が存在しない国もある。
納税
A1から国Aが銀行経由で徴税を行う場合を考える。
- A1は預金を失い、租税債務を解消する。
- 銀行はA1の債務を解消し、準備預金を失う。
- 中銀は銀行の預金債務を解消し、政府の預金債務を負う。
- 政府は準備預金(国庫)を獲得し、A1への課税請求権を失う。
A1:
| 借方 | 貸方 |
|---|---|
| 租税債務100 | 預金100 |
X銀行:
| 借方 | 貸方 |
|---|---|
| 預金100 | 準備預金100 |
中銀:(この行もなくてよいが、便宜的に書いておく)
| 借方 | 貸方 |
|---|---|
| X準備預金100 | 国庫100 |
A政府:
| 借方 | 貸方 |
|---|---|
| 国庫100 | 租税債権100 |
銀行が直接支払いを代行しないそれ以外のルートであっても、国庫が準備預金(中銀預金債権)として租税を受け付ける以上、課税者の保有現金そのものが減るか、課税者の預金とその銀行の準備預金の両方が減るかのどちらかが起きる。つまり、マネーサプライとベースマネーの減少が同時に起きる。 (課税者が"最初から"現金を持っている可能性は低いため、概ね預金と準備預金の同時消滅が起きる)このため、租税支払いの時期には準備預金需要が上昇する(コールレートが上がる)ことがある。
国債発行
政府は、国債を発行できる。日本では財政法5条によってこれが制限されており、中銀の国債直接引受を行うには国会で議決する必要がある。中銀が引き受けた場合、その購入額が国庫に準備預金として振り込まれる。中銀が引き受けない場合は市中消化となり、市中銀行に購入をオファーすることになる。
中銀引き受けの場合は、もっとも簡単である。
中銀:
| 借方 | 貸方 |
|---|---|
| 国債100 | 国庫100 |
政府:
| 借方 | 貸方 |
|---|---|
| 国庫100 | 国債100 |
市中引受の場合、大きく分けてそのまま市中銀行が保有する場合と、中銀が回収する場合がある。
X銀行:
| 借方 | 貸方 |
|---|---|
| 国債100 | 準備預金100 |
中銀:(なくても良いが、便宜的に書いておく)
| 借方 | 貸方 |
|---|---|
| X準備預金100 | 国庫100 |
政府:
| 借方 | 貸方 |
|---|---|
| 国庫100 | 国債100 |
中銀が回収すれば、これに加えて次を連結する。
この結果として先の直接引き受けと同様のポジションになる。
しかし厳密には中銀による直接引き受けと、市中銀行での消化+中銀の買い入れには微妙な違いがある。国債の中銀直接引き受けに対して、市中消化の場合は、一旦市中銀行に買わせるために、市場に見合った金利を付与する(額面より低い価格で売る)必要が出てくる。 しかし、中銀が金融緩和で国債買い入れを行っている間は、中銀の購入額よりほんの僅かに安くすれば裁定機会となるため、この摩擦を無視できるようになる。
市中銀行への売却は中銀の買いオペで相殺できるとしたが、実際には中銀が最初に既発国債を買い入れて市中銀行に購入資金を用意してから、上記のような購入手続きを踏み、最後に逆操作を行うというように更に追加の手続きを挟むことでコール市場への影響を減らす工夫をすることもできる。
国債償還
政府は、国債を満期に償還する。国債は個人でも保有できるが、大半は公私の金融機関や中銀によって保持されている。
償還手続きは先と逆のことをすればよい。中銀保有が最も簡単である。
中銀:
| 借方 | 貸方 |
|---|---|
| 国庫100 | 国債100 |
政府:
| 借方 | 貸方 |
|---|---|
| 国債100 | 国庫100 |
X銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 国債100 |
中銀:(なくても良いが、便宜的に書いておく)
| 借方 | 貸方 |
|---|---|
| 国庫100 | X準備預金100 |
政府:
| 借方 | 貸方 |
|---|---|
| 国債100 | 国庫100 |
政府支出(財政政策)
政府は税制によって(貨幣需要を固定すると同時に)、市中から預金および準備預金を回収する。 また、政策上の公共事業発注や社会福祉政策などで、市中へ預金および準備預金を注入する。
これは政府によって実行され、したがって法的強制力を持つ。国庫と市中預金者および市中銀行とのやりとりを財政政策と呼ぶ。
- 政府は国庫を失い、望んだ政策を得る。
- 中銀は政府への国庫債務を解消し、銀行の準備預金債務を負う
- 銀行は準備預金を獲得し、預金者(政府受注者)の預金債務を負う
- 受注者は預金を獲得し、政策実行負担を負う。
政府:
| 借方 | 貸方 |
|---|---|
| (政策)100 | 国庫100 |
中銀:(なくても良いが、便宜的に書いておく)
| 借方 | 貸方 |
|---|---|
| 国庫100 | 準備預金100 |
X銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 預金100 |
A1:
| 借方 | 貸方 |
|---|---|
| 預金100 | (政策実行負担)100 |
ここでの政策は、(例えば給付金のように)移転的な場合もある。移転的であれば、受注者の政策実行負担は名目的なものになる。納税の場合とは逆に、支出先の市中預金と、その口座を抱えている銀行の準備預金が支出分と同額増える。
中銀金利政策(金融政策)
中央銀行は、ここに預金をもつ市中銀行に対して、準備預金を融資したり、国債などの金融資産の売買を持ちかけることができる。その支払いは準備預金、つまり自身の債務の解消によって受ける。売買はあくまでオファーによるものなので、別段の定めが無い限り、望んだ価格で市中銀行に買わせたり売らせたりはできず、例えば売却先が望む金利が生じる価格で売買する必要がある。
中央銀行による対金融機関の金融資産売買によって準備預金やコールレートに影響を与えることを金融政策と呼ぶ。
売却時
中銀:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 国債100 |
X銀行:
| 借方 | 貸方 |
|---|---|
| 国債100 | 準備預金100 |
買入時
中銀:
| 借方 | 貸方 |
|---|---|
| 国債100 | 準備預金100 |
X銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 国債100 |
銀行は業務に必要最低限の準備預金は確保しようとするが、過剰な分は融資や金融資産に回そうとするなど、自身の業務にとって適切な水準に保つ動機がある。 中銀が国債や金融資産の売却で準備預金を解消した場合、準備預金の需要が高まるので、一般にコールレートは上がり、逆に中銀がこれらの購入する場合、コールレートは下がると考えられている。
貿易決済(TBA)
色々決済手段あるようでややこしく、調べられなかった。わかったら追加するかも。
よくある怪しい論点
信用創造における又貸し説
しばし経済学の教科書に載っている(こともある)又貸し説とは、次のようなものである(ただし、「又貸し説」という名称はこの説に対する批判的ニュアンスを含んでいるので、当然ながら記載文献はこれを又貸し説とは呼ばないことが多い)。
- 預金者1が銀行B_1に現金Xを預け入れる。
- 銀行B_1は預金者1の預金からX(1-r)を預金者2に貸し出す。
- 預金者2は銀行B_2に現金X(1-r)を預け入れる。
- 銀行B_2は預金者2の預金からX(1-r)(1-r)を預金者3に貸し出す。 ...
これによって総預金が1-rの幾何級数で増やせる、というものである。
筆者の考える限り、この又貸し説は、次の3点で現実から乖離しており、このせいでマネーサプライとマネタリーベース、および準備預金制度の間にあまりに強い関係を見出してしまっている。
- 「預金」と「預け入れられた現金(準備預金)」を区別していない。
- 「融資」と「現金貸し出し=(融資+融資全額出金)」を区別していない。
- 銀行および中銀のなす決済業務が考慮に入っていない。
この説明では、融資は現金貸し出しそのものになっており、また預金とは預け入れられた現金そのものを指している。これは現実の銀行業務を反映していない。
預金とは銀行の負う出金債務のこと であって、預け入れ現金とは明確に別物である。したがって、「預金を貸し出す」というのは会計上意味不明な表現であり、これが「又貸し説」という名称を動機づける。融資も現金の貸し出しではなく、やはり銀行の預金債務の発行でしかない。このため、手元に現金がなくとも融資を行える。また、銀行は送金決済業務を通常出金なしで実行でき、銀行間送金であっても中銀とコール市場の支援のもと、変動を吸収しつつ行うことができる。
又貸しの観点では、例えば、
- 預金者1が、預金者2への送金のために銀行B_1から預金を下ろそうとする。
- 預金者2が、銀行B_1の準備預金以上の融資を希望する。
場合、どちらも不可能になる。しかし現実の銀行はこのどちらも可能である。
- 預金者1の、預金者2の送金要求にしたがって、コール市場で準備預金を調達し、これを銀行B_2に振り返る。
- なお、B_2 = B_1の場合、準備預金に全く触れずに送金を達成できる。
- 又貸し説の銀行は、B_2 = B_1の場合でも送金業務を代行していなければ達成できない。
- 預金者2の口座に、(準備預金以上の)金額を記帳する。
準備預金以上の融資を実行したとしても、銀行が高額送金決済の多くを業務として代行している以上、その全額の出金が要求される可能性は非常に低い。したがって、銀行は準備預金を超える融資を実行しても、預金債務デフォルトを避けられる。
又貸し説のもう一つ問題点は、準備預金率が所与の数値として外生的に与えられており、これによって、預金総額の上限が決まってしまう、つまり 預金を外生的パラメータで制御できるかのように錯覚する 点である。実際には、必要な準備預金とは、預金総額に対して決済システムが出金需要に応じられるかどうかによって決まるものだし、またそもそも(預金の相当部分をなす)融資は資金需要がなければ発生しない という一方向性があるので、準備預金を増やしたからといって融資が一定比率で増えるとは限らない。しかし又貸しモデルは融資総額と準備預金・準備率にあまりに簡単な関係を導いて"しまう"。
じつのところ、準備預金制度は、銀行に営業上必要な準備預金を確保するインセンティブを与えるガイドラインとして唯一ののものではない。 カナダは準備預金率がゼロであり、その代わり、公定歩合による自動貸越(準備預金が枯渇した場合、自動で利子付き融資が発動する)が設定されていることによって、準備預金を0以上にするインセンティブを設けている。準備預金制度があるから銀行は準備預金を持つのではなく、銀行は出金・送金需要に応じられるだけの準備預金(の調達手段)を持つ必要があり、そのガイドラインとして準備預金制度を設定する場合がある、というだけである。
民間預金が国債発行/貸し出し原資?
「我々の預金によって、国債が買われている、または銀行融資の運転資金となっている」という誤解は根強い。 しかしすでに見たように、国債の購入原資は準備預金であり、銀行にとっては市中預金者の預金は債務、つまり負債であって支払い原資ではない(銀行や中銀やその他金融機関以外の個人が国債を購入することもできるが、割合でみればそれは少ないので無視している)。 そして、銀行融資は口座記帳による信用創造であり、準備預金は、それらの出金需要に答えられるだけあれば十分である。 預金と準備預金の間には(又貸し説のような)簡単な関係はなく、それぞれの総量は保存もしていない。そのため、我々の預金と準備預金(国債購入原資or銀行運転資金)の間に、そのような単純な関係はない。
そうは言っても、我々はしばし物理的な現金を引出して使ったりするため、我々は根源的な現金を持っていて、それを預けていることで、 国債購入原資また運転資金である準備預金を銀行または中銀または政府に「与えている」と思うかもしれない。
「我々が現金を預け入れることによって、銀行は融資や国債購入のための準備預金を得ている」という認識が成り立つためには、実際に我々自身が何らかの方法で現金を獲得し、それを銀行に預け入れている必要がある。しかし、よくよく考えてみれば、そのようなことは起きていない。
なぜなら、 我々の収入も、通常銀行預金として振り込まれるからだ。 我々は労働や商取引の結果、現金を得ているのではなく、預金を得ている。そして、我々はその一部を出金、つまり銀行の準備預金を削ることでそれを現金化しているのであって、それをふたたび預けた(あるいはそもそも出金せずにそのままにした)ところで、もとに戻っただけである。もしあなたの給与が現金支払だったとしても、それはあなたの勤務先企業の預金を現金化してあなたに配ったというだけである。出金は準備預金を減らすから、もしあなたが現金で受け取った給与を預金しなかったら、あなたが働いて収入を得ることによって、銀行は準備預金を失ったことになり、あなたがその給与を再び銀行に預け入れたなら、やはりもとに戻っただけである。あなたの労働と預金はトータルで何一つ準備預金に寄与していない。
我々は紙幣の発行者ないし生産者ではない以上、 我々が労働によって現金を生み出すことはありえない。 (もし現金を生み出していたなら、それは通貨偽造である)。 この意味で 「我々の預金が準備預金に寄与している」というのは思い上がり であって、市中銀行と中銀の信用創造の結果、偶然我々の手元に(総預金に比べれば僅かな額が)物理的紙幣の形をとって存在していると考えたほうが自然である。 つまり、市中銀行は融資によって、我々に現金を引き出す権利を付与し、中銀は政府公債によって獲得した国庫及びそれが振り返られた各市中銀行準備預金の債務を履行することで、物理的に現金を供給している。 この経路なしには我々はそもそも合法的に現金を手にすること自体が不可能である。
ただし、あなたが多額の預金を持っていて、それを普通預金から定期預金に切り替えたなら、定期預金については準備預金率は小さく設定されているので、その金額×準備預金率の差 だけ、銀行の準備預金に寄与することはできるかもしれない。しかし、一般に銀行の準備預金は預金総額に対して非常に小さい。典型的にはあなたが1000万円を普通から定期に振り替えたところで、銀行は数万円の準備預金の余裕を得るに過ぎない。
このように預金と準備預金を峻別すれば、民間投資と国債が限られた資金を取り合っている、という単純な観点が間違っているとわかる。しかしこの峻別をしてもなお、国債の発行が民間投資に影響するという可能性は残っている。つまり、国債を市中銀行に向けて売却した場合、準備預金が減るのだから、コールレートが上昇し、間接的に民間融資が渋くなる(融資を絞る/金利を引き上げる)という可能性である。このクラウディング・アウトの是非については次で検討する。
クラウディング・イン/アウト
政府が国債を売却した場合、コール金利の上昇、または民間預金の減少(民間投資の減少)が起きるという説がある(クラウディング・アウト)。一方、コール金利の低下、逆に民間預金と投資の増加が見込めるという説もある(クラウディング・イン)。
これは、両者の論者が、国債発行による政府支出に伴って 「金融政策がどのように従属して振る舞うか」という、いわば制約条件を違えていることに最大の食い違いがある。
クラウディング・アウトのロジックとしては概ね以下のようなものである:
- 政府が国債を大量に売却する場合、売り抜けるために高い金利を付与する。具体的には、購入者である市中銀行が準備預金を手放してもよいと思う程度の高金利で売却する。
- これによって市中銀行は準備預金を減らして、利回りのいい国債を購入する。
- 準備預金が減少するため、準備預金のバッファであるコール市場のレートが上昇する。
- 銀行の資金繰りが厳しくなるため、融資が抑制的になる。
これについて2つ指摘できる点がある。
中銀の金融政策が行われないという悲観的前提
まず1つ目として、中央銀行は、その目的からして金利の調整を掲げている。つまり、中央銀行はこのような場合に、政府の国債売却に伴って、その反動を吸収する金融政策を実施できるし、するはずである。 中銀は単に国債を政府の売却額よりわずかに高い値で買い続ければよい。このとき、市中銀行にとっては裁定機会が発生するから喜んで任意の国債を購入して中銀に再び売却する。この場合、結果的に市中銀行は準備預金を減らす必要がないので、金利上昇を抑制できる。最終的なポジションは、中銀は国債と準備預金債務を抱え、政府は国庫を手にしたのみである。つまり、国債発行に伴って金融政策が連動することによって、財政法の公債中銀引受制限を実質的に無効化できる 状況が出現しうるが、そうした金融政策を考慮に入れていない。中銀がその金利目標に向けてオペレーションを行う限りにおいて、政府の国債売却による利上げ圧は中銀に吸収される(=市中銀行の準備預金の枯渇も防がれる)ので、上記クラウディング・アウトのロジックは途中で止まり、結局民間の投資資金には影響しないことになる。
国債発行益による政府支出
2つ目は、政府が国債発行で得た資金をそのままにはしないだろうということである。もし国債発行益で国債償還をするのなら、トータルでは何も変わらない。発行益を国庫に放置するなどという無意味な行いも当然考えられない。したがって、通常政府は得た資金をまるごと使って支出(財政政策)を行うはずが、このときは市中預金者と市中銀行の両方の預金に政府支出が振り返られることになる。その額はもちろん国債発行額そのものだから、結局市中銀行が国債購入で失った準備預金はトータルでは戻ってくる。 さらに政府の発注を受けた民間事業者の預金はこれによって直接増えている。
これは実際に仕訳を連結することでも理解できる。まず、政府が市中銀行で国債を売却したとする: 銀行:
| 借方 | 貸方 |
|---|---|
| 国債100 | 準備預金100 |
政府:
| 借方 | 貸方 |
|---|---|
| 国庫100 | 国債100 |
政府は獲得した国庫で支出をする。
政府:
| 借方 | 貸方 |
|---|---|
| (政策)100 | 国庫100 |
銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 預金100 |
A1:
| 借方 | 貸方 |
|---|---|
| 預金100 | (政策実行負担)100 |
これを連結すると
政府:
| 借方 | 貸方 |
|---|---|
| (政策)100 | 国債100 |
銀行:
| 借方 | 貸方 |
|---|---|
| 国債 100 | 預金100 |
A1:
| 借方 | 貸方 |
|---|---|
| 預金100 | (政策実行負担)100 |
となり、銀行は準備預金を失っていないし、それどころか国債という金融資産を得ている。もちろん、銀行の預金債務は増加したので、増加した送出金需要のために、銀行は同額の国債よりも準備預金を欲しがるようになるかもしれない。その時はやはり準備預金需要の増加=コールレートの上昇として現れることになり、中銀の金利政策によって、必要な分の準備預金が供給される。そうしたならば、結果的に準備預金と預金の両方が増えたことになる。(預金債務の増加に対して"必要な"準備預金の増加は小さいので、ここで得た国債を全額売却する必要は無い)。そして銀行が準備預金をどうバランスさせようが、民間預金者の預金は赤字支出の分だけ増えており、資金圧迫どころか資金提供していることになる。
したがって 国債発行に対する中銀金融政策の振る舞い、および政府のその後の財政支出を考慮に入れれば、むしろクラウディング・インが起きえる。 クラウディング・インなのかアウトなのかは、金融政策をどう連動させるか、国債で得た資金による支出をどう行うか(誰に対して行うか)によって変わることになる。クラウディング・アウトのロジックは、中銀金融政策が政府の財政政策に対して敵対的かつ、政府が国債発行益を国内支出に使わないという、極めて悲観的な状況を想定しなければ当然のものとは言い難い。しかしこれは奇妙な前提だ。 中銀と政府が自国経済に敵対するシチュエーションを当然視しなくてはならない理由がどこにあるのか? (政府および中銀関係者が単に愚かであるという可能性はゼロではないが)
実のところ、政府が巨額の財政支出を行った場合に民間と競合するのは、民間の資金ではなく、実物財のほうである。上記の仕訳でもわかるように、政府の国債発行と支出の結果、民間では預金が増えるが、受注した政策の実行負担は発生している。巨額の公共事業発注を行うことで、それと資源や労働力を取り合う分野のコストアップやインフレや賃金上昇が起きることはあり得る。
市中銀行と中銀の破綻可能性
市中銀行は、破綻する可能性がある。破綻というのは要するに債務不履行である。具体的には、準備預金の資金繰りに失敗し、コール市場で借りた資金を返済できなくなる、預金の出金に応じれなくなる、などがそれである。中銀の融資(特融)によって救済されることもあるが、問題が大きい場合は解散となる場合もある。この理由は、銀行の預金債務は、日本銀行券に関するものであって、銀行はこれを送金したり融資を受けたりすることはできるが、自身で日本銀行券を発行することはできないからである。市中銀行が不当な融資を連発した場合、その預金が自行の内部で出回るだけならよいが、通常送金決済などで外部に漏れていく。この融資を回収できなかった場合、それは準備預金の減少につながる。
その点、中銀は自身の準備預金債務による破綻の可能性は無い。準備預金の債務履行とは、貨幣=中央銀行券の発行であり、これは常に履行できる。貨幣債務の履行は新しい貨幣の発行なのでこれも当然履行できる。もちろん、これ以外の場合、例えば外貨建て債務を抱えつつ、履行するための外貨が不足した場合は破綻があり得る(しかしこれは中銀に限ったことではない)。
国債デフォルト(財政破綻)を"起こせるか"
論理的には、やろうと思えば起こせる。政府が国債を高金利でも売却できず、既発国債の償還資金を得られなかった場合。国債デフォルトする。しかし、すでに見たように、中銀が金融政策で国債購入をすればいつでもこれは回避でき、かつ金利への影響も抑制できる。 また、日本の場合、市中消化せずとも国会議決で中銀引受させることもできる。これはどちらでやっても最終的なポジションは同じことである。逆に言えば 政府が「償還を行わない」という自爆ボタンを押して実際に償還を無視すれば、政府は破綻"することができる"。 これをあえて選ばなければ国債デフォルトは起きない。
中銀が(最終的に)国債を引き受ける、ということは、貸付債権の代わりに国債を受けることで政府への融資(信用創造)を行っていると考える事ができる。償還資金を新規国債発行で得る操作は要するに借り換えのことである。
これは、「市中銀行が自転車操業の企業に融資を繰り返す」ことに似ているように見えるが、微妙に異なる。市中銀行が倒産しそうな民間企業に融資を繰り返すことが憚られるのは、それらの流出によって銀行自体の準備預金が目減りし、資金繰りが悪化することと、預金を回収しそこねた場合に損失を出すことによる。したがって、市中銀行は相手の「真の信用」を見積もり、融資に値するかどうかを適切に判断しなければ、自身が損失を被る。
しかし、中銀の場合は自身の預金債務が増えても、それは常に履行できる。中銀の預金債務は、中銀にとっては痛くも痒くもない。また、中銀による政府融資は、融資し続ければ常に以前の融資(国債)を回収(償還)できるので、貸し続けること自体によって貸し倒れを防止できる。これが成り立つのは、中銀紙幣が信用ピラミッドの頂点にいるからである。中銀の与信とは「融資先の信用を見積もってそれに見合った融資を行う」のではなく「中銀が与信した対象に融資額の額面価値がつく」 のであり、市中銀行が「この者は本当にX円の融資に値するのか」を判断するのに対して、中銀は「この者の支出の価値がX円だと定義してよいのか」を判断している。
何れにせよ、中銀には政府債務をあえてデフォルト"させる"動機がない。もちろん政府にもその動機はない。 一体誰が国債デフォルトを望むのか? 少なくとも国内関係者の誰一人として望まないだろう。国債デフォルトを望まないのであれば、国債を借り換えし続けることになり、それは実際可能である。そしてこのことが、政府の財政制約を事実上開放する。
プライマリーバランス黒字化の会計的意味
これはクラウディング・アウト/インと重複する話でもある。
いわゆるプライマリーバランスの黒字化というのが財務省関連団体によって唱えられている。 プライマリーバランスとは、端的に言えば、国債発行収入以外の歳入と、国債償還費用以外の歳出の差額である。国債を発行して償還する分にはそれらは(利払いを無視すれば)単に借り換えたようなものなので、税収と支出の差額といって良い。黒字化とは、税収>支出のことであり、赤字とは税収<支出を意味する。歳入と歳出はバランスしているから、この差額は正味の新規発行国債(=支出ー税収)または、正味の償還した国債(=税収ー支出)の額に一致する。つまり、国庫に入れたままで翌年に繰り越す分を無視すれば
ということを意味する。したがって、会計上はこれまでに述べた操作の合成として理解できる。つまり、それぞれの仕訳を単に連結すればよい。
税収は民間預金と準備預金の減少であり、支出は民間預金と準備預金の増加となる。また、国債の主要な保有者は中銀か市中金融期間である。したがって政府が赤字や黒字を出したときに会計上何が起きているのかを考えるにあたり、想定すべき挙動は4つある。
赤字支出
銀行:
| 借方 | 貸方 |
|---|---|
| 国債100 | 準備預金100 |
政府:
| 借方 | 貸方 |
|---|---|
| 国庫100 | 国債100 |
政府はこれを使って同額の支出を行う。
政府:
| 借方 | 貸方 |
|---|---|
| (政策)100 | 国庫100 |
銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 預金100 |
A1:
| 借方 | 貸方 |
|---|---|
| 預金100 | (政策実行負担)100 |
連結すると以下
政府:
| 借方 | 貸方 |
|---|---|
| (政策)100 | 国債100 |
銀行:
| 借方 | 貸方 |
|---|---|
| 国債100 | 預金100 |
A1:
| 借方 | 貸方 |
|---|---|
| 預金100 | (政策実行負担)100 |
つまり、民間預金は増加し、銀行は国債を得る。 この段階から銀行が国債売却を望むか、または最初から政府が市中消化の代わりに中銀直接引き受けを使っていた場合、これに次が連結される。
銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 国債100 |
中銀:
| 借方 | 貸方 |
|---|---|
| 国債100 | 準備預金100 |
そして最終ポジションは以下。
政府:
| 借方 | 貸方 |
|---|---|
| (政策)100 | 国債100 |
銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 預金100 |
中銀:
| 借方 | 貸方 |
|---|---|
| 国債100 | 準備預金100 |
A1:
| 借方 | 貸方 |
|---|---|
| 預金100 | (政策実行負担)100 |
つまり、準備預金も民間預金も増えている。
黒字償還
納税と国債償還を連結する。 まずは市中銀行の国債償還を行う。
銀行:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 国債100 |
政府:
| 借方 | 貸方 |
|---|---|
| 国債100 | 国庫100 |
このコストを税収で賄う。
A1:
| 借方 | 貸方 |
|---|---|
| 租税債務100 | 預金100 |
銀行:
| 借方 | 貸方 |
|---|---|
| 預金100 | 準備預金100 |
政府:
| 借方 | 貸方 |
|---|---|
| 国庫100 | 租税債権100 |
連結すると以下
政府:
| 借方 | 貸方 |
|---|---|
| 国債100 | 租税債権100 |
銀行:
| 借方 | 貸方 |
|---|---|
| 預金100 | 国債100 |
A1:
| 借方 | 貸方 |
|---|---|
| 租税債務100 | 預金100 |
つまり、民間預金は減少し、銀行は国債を失う。 預金債務を減らした銀行が、余った準備預金で国債を購入しようとするか、または最初から召喚する国債を中銀が持っていた場合は、次を連結する。
銀行:
| 借方 | 貸方 |
|---|---|
| 国債100 | 準備預金100 |
中銀:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 国債100 |
最終ポジションは以下
政府:
| 借方 | 貸方 |
|---|---|
| 国債100 | 租税債権100 |
銀行:
| 借方 | 貸方 |
|---|---|
| 預金100 | 準備預金100 |
中銀:
| 借方 | 貸方 |
|---|---|
| 準備預金100 | 国債100 |
A1:
| 借方 | 貸方 |
|---|---|
| 租税債務100 | 預金100 |
つまり、民間預金と準備預金がともに減少している。
以上から、政府赤字および黒字において、民間預金者と銀行の保有する金融資産がどうなるかが次のようにまとめられる。
- 赤字で国債を市中銀行へ発行し、支出する:
- 民間:預金増
- 銀行:預金債務と国債の対生成
- 赤字で国債を中銀へ発行し、支出する:
- 民間:預金増
- 銀行:預金債務と準備預金の対生成
- 徴税し、黒字で市中銀行国債を償還する:
- 徴税し、黒字で中銀国債を償還する:
- 民間:預金減
- 銀行:預金債務と準備預金の対消滅
つまり、政府黒字は民間の金融資産を常にへらす。 政府が黒字によって国債を償還するということは、単に我々の預金や銀行の準備預金と国債を対消滅させることである。 銀行にとっては国債または準備預金と預金債務がペアになっているので、損も得もしないように見えるが、一般に銀行の預金債務に対して必要な準備預金の額は小さい(準備預金率が1%程度であることを思い出そう)ので、同額対消滅するほうが資金繰りは悪化する。
経済を拡大させたければ、そこに流通する貨幣が当然必要となるが、会計上それを供給可能なのは政府の赤字だけである。政府黒字とは比喩でもなんでもなく貨幣破壊を意味する。
バブル景気には政府黒字が達成できたという話があるが、上記の会計的事実と組み合わせれば、それは民間が不釣り合いな債務を抱えることで好景気を無理やり達成していたことだとわかる。つまり、好景気と政府黒字が両立した場合、それは民間の債務超過による崩壊のシグナルである。
本邦にはPB黒字化を唱える熱心な団体が存在しており、筆頭が財務省である。驚くべきことに、企業経営者団体である経団連も度々PB黒字化を唱えている。
金利の行方
ここまでの議論では金利を無視していた。市中銀行及び中銀が、融資や国債の金利をどのように処理しているかを考えておく。
まず、市中銀行が融資を実行した場合。融資を受けた預金者は、その返済日までに、自身の預金口座に、融資額に金利を添えた金額を用意する必要がある。これが滞りなく行われた場合、市中銀行は貸付債権と、この預金者の預金債務を相殺させる。
このとき、金利が掛けられているのだから、融資の段階で銀行が負った預金債務よりも、返済日に銀行が解消した預金債務のほうが大きい。金利(および振込み手数料)は、銀行の主たる収入手段だが、ここで重要なのは、この営業プロセスに準備預金(現金)操作が現れていないということである。銀行は入金によって利益を得ているのではなく、預金債務(負債)の圧縮によって利益を得ている。 ところで、債務が消滅するということは、マクロ的にはマネーサプライの消滅である。つまり預金貨幣が消滅したことになる。そこで、銀行は預金者の利払いで消滅した債務の分、銀行員への給与支払いを信用創造によって行う。 通常銀行員は入行とともに、給与振り込み用に自行の口座を開くことになっているが、その理由がこれである。この信用創造は融資とは違い、特に返済義務のない、純粋なキーストロークである。
これ以外にも国債を償還したときの利益があるが、この場合は準備預金の側が増えることになる。市中銀行が準備預金を増やしたということは、抱えられる預金債務枠が増えたということでもあり、同様に信用創造を行う余地が発生する。
中央銀行の場合、公定歩合での準備預金貸し出し、または国債の償還がその利益となる。ここでも同様の状況が発生する。つまり、利付き国債を購入したり、特融による貸付債権を得て、それを償還ないし返済を受けたとき、それは国庫か準備預金との対消滅によって行われる。そして利付なのだから、それは国債購入時や特融を行ったときのベースマネー信用創造の額よりも大きい。つまり、ここでも中央銀行が金利によって利益を上げるということは、中銀の準備預金/国庫債務の圧縮という形を取っている。
中銀職員の給与はここから各職員の口座がある市中銀行への振替という形で支払われる、つまり再度信用創造によって準備預金債務と預金債務を生み出す。しかし中銀は金融システムの頂点にある都合上、職員あたりの利益は市中銀行よりも大きくなるが、それだけ中銀職員の給与が大きくなるというわけではない。では余った利益はどこに行くのか?
中銀の立場からすれば、この利益というのは債務の削減だから望ましいように見えるが、経済全体からすればベースマネーの消滅であって、必ずしも望ましいとは限らない。日本の場合、ここで設定されているのが、国庫納付金 という枠である。つまり、中銀(日銀)が得た利益から、給与や経費などを支払った残りの利益は、国庫に戻ってくる。
「国庫に戻る」というが、これも信用創造である。市中銀行同様、中銀が利益を上げるということは、その債務の消滅を意味するが、これが非随意に起きるのを防ぐため、消滅した債務分、再度国庫への信用創造を行うことで再度ベースマネーの供給にまわすことになっているのだ。
「国債の金利支払いによって財政が圧迫される」というのは、これまでの話のように、そもそも財政上の制約が存在しないのだからもとから杞憂である。しかし政府が国債の利払いを行ったとして、それはどこにいくのか、という疑問はある。その答えがこれである。償還が対金融機関であれば、それは金融機関の利益となる。その金融機関が準備預金を持て余すようなら、中銀が金融引締で準備預金を回収するだろう。償還が対中銀であれば、中銀が債務圧縮という意味で利益を得るが、その利益は再び国庫への信用創造の形で変換される。つまるところ、国債金利支払いがどれほど高額になろうとも、そのことよって将来の国庫が消滅する心配はない。中銀が国債金利の利益をあまりにももらいすぎたなら、それは国庫に返ってくるからだ。
一人あたり「国の借金」論
しばし国債残高を国民一人当たりの借金として換算する飛ばし記事が書かれることがある。すでにこのナンセンスさは何度も方方で指摘されていると思われるので詳しく書かない。国債残高が国の借金であるというのはそのとおりである。しかしその実質的な意味は、(国債残高が増え始めた時期=変動相場制採用以後に)政府および中銀から供給されたベースマネーのことである。 我々の経済は、ベースマネーと、それを元に銀行が信用創造した預金によって成立している。すでに述べたように、国債を黒字償還するということは貨幣の破壊のことにほかならない。仮に一人あたり国の借金が900万だとして、これを(租税によって)完済するということは、すべての企業や家計の預金から一人あたり900万を徴収し、国債と対消滅させるということである。
では財政均衡(赤字でも黒字でもない状態を短期的にせよ長期的にせよ目指すこと)はどうなのか、というと、一見無害で中立的に見えるが、これも非現実的だろう。経済は基本的には発展しようとする。50年前と現在では、仮に人口を考慮に入れたとしても、身の回りの製品や商品の価格は(もちろん性能も)上がっている。上がらなければそうした製品開発や改善のインセンティブが存在しないことになるので、上がっていなければまずい。そして上がっているということはその取引を行うための貨幣が供給されていることになる。これを銀行の信用創造だけで賄うのは預金債務が増えすぎて不可能だろうから、結局政府が赤字によって供給する以外にない。つまり、国債債務残高は、増え続けるのが平時の挙動である。
金融緩和の有効性
金融緩和とは、中銀が市中銀行から国債等金融資産を買い上げることで、市中銀行に準備預金を供給することをさす。金融引締はこの逆である。緩和を実行すると中銀は準備預金を持て余すようになるためコールレートは低下する。準備預金に余裕ができることにより、銀行は融資を行う余裕を持つことになる。いわゆるリフレ派は、金融緩和によって景気回復と物価の向上が起こせると主張し、これを推進したが、実際には、ベースマネー(金融緩和によって直接供給される)に対するマネーサプライの比である貨幣乗数は、2013の金融緩和開始から一貫して下がっている。つまり、ベースマネーの供給に見合ったサプライを生み出せていない。これは金融機関に準備預金が死蔵されていることを意味する。更に2016からは準備預金の超過分についてマイナス金利をかけるようにすることで、融資をしなければ準備預金が目減りするという負のインセンティブを設定したが、依然として貨幣乗数は好転していない。
この振る舞いを把握するにあたって 金融緩和によって直接供給できるのはあくまで準備預金だけであることに注意が必要である。準備預金は経済活動に用いられる貨幣ではないのでこれが増えてもそれによってだれかの購買力や需要が向上するわけではない。 また、準備預金のコールレートや公定歩合と、銀行が融資する際の金利は別物であり、コールレートが下がったからと言って必ずしも銀行金利がそこまで下がるとは限らない。そもそも、銀行が準備預金を獲得して融資のための余裕を持てたからといって、融資を望む預金者が居なければ融資は発生せず、マネーサプライ=我々の預金は増えない。銀行はあくまで資金需要に応じるのであって、預金者に無理やり貸し付けることはできない。すでに批判した又貸し説では、準備預金制度によって、マネーサプライとベースマネーに極めて単純な乗数関係を導いてしまうが、実際には乗数関係は変化し、ベースマネー増にサプライは追従しきらない。こうした金融政策の機能不全は、MMTerが財政政策を重視する動機の一つにもなってると思われる。というのも一方の財政政策は(きちんと赤字をだして支出すれば)準備預金と同時に直接民間預金を確実に増やすことができるためだ。
中銀引受け/債務拡大の是非について
まず中銀引受自体は、それが直接引き受けにせよ市中消化と買いオペの連動にせよ、大規模な政変が起きるなどを除けば、永久に可能である。その額にも、理論上の制限は無い。金融政策が財政政策に連動する限り、これは常に実行できるし、あるいは中銀が金融政策を実施しなくても、国会の議決によってこれを強制できる。制限はないので、 100兆でも100垓でも100極でも、会計上は発行および中銀引受させることは可能だし、その事自体が直接なんらかの問題を引き起こすということはない (もちろん、そのように調達した資金でどのような政策を実行するか、またはしたかは問題になる)。
しかしながら中銀引受は政治的には忌避されることがある。しばし、中銀の直接引受が財政法で制限されていること、また現在の中銀オペレーションの金融緩和が例外的であっていずれ"出口"(金融緩和の終了:国債購入を控え始める)が求められていることの理由として、「政府の財政節度を保つため」 というのが挙げられる。つまり、政府が際限無く資金を調達できるとなると、何をやらかすかわからないため、あえて回りくどい手続きを設けているということになる。
逆に言えば、中銀引受そのものを忌避する直接的な理由はあくまで政治的な理由であって財政的理由ではない ということだ。政府が中銀引受で獲得した資金で、特段国民経済に問題のない(あるいは有益な)財政政策を実行したなら、それは文字とおり問題がない。極端な話、100垓円の国債を中銀に引き受けさせ、現金として引出し、誰もアクセスできない地下にタイムカプセルとして償還日まで埋める(または永久に埋め立ててしまい、国債は借り換え続ける)政策は、大量の国債を発行するものの、毒にも薬にもならないので無害である。例えば財政法の背景として、戦時に大量の国債を発行して中銀引受させ、戦費調達をしたという歴史がある。仮にこれが望ましく無い政策だったとしても、それは政策の問題であって、中銀引受それ自体が問題ということにはならない。 では一体望ましい政策はなんであるか、またどういう政策であれば実施しても問題がないと言えるか、というのは当然よく検討する必要がある。しかしいずれにせよ、政治的対立を無視すれば、基本的に政府+国会は、予算制約を一切気にすることなく、その政策を実行した場合の国民経済への影響のみを考慮して政策を実施する余地が常にある。 一つ釘を差しておくとすれば、「政策のX円あたりの効果」というのは間違った評価指標である。
政府債務が拡大することを忌避する動機は、おそらく民間企業の財務評価のアナロジーから来ていると考えられる。つまり、巨大な債務を抱えており、経常赤字を出していて、自己資本率が低い場合、投資家はそうした企業には投資しないだろうというものだ。しかしこのアナロジーは成り立たない。すでに見たように政府は債務を常に履行できる。万が一このことを理解しない投資家が巨大な主権通貨債務を抱える国の国債を保有していて、破綻リスクを恐れてそれを手放そうとしても、中銀はこれを悠々と回収できるため、金利上昇を抑えられる。
MMTerのスローガンで「政府赤字は民間黒字」というのがあるが、これは何もMMTerの過激発言ではなく、会計的な事実である。つまり、「MMTerの」という修辞は余計である。そして政府赤字は国債によって発生するのだから、貨幣そのものを消滅させる気でもない限り、国債はそもそも償還しない(借り換え続ける)ことを前提としなければならない。
このことは、「上記の中銀システムをまっさらな状態から始めるにはどうすればいいか?」 を考えればよく分かる。預金者の市中銀行口座残高と市中銀行の準備預金残高と国庫がすべてゼロであり、誰も日本銀行券を保有していない状態から、どうすれば金融を始められるだろうか?
市中銀行が信用創造をしても、中銀が準備預金を供給しなければそれは履行できない。政府が国債を売却しようとしても、市中銀行が準備預金を持たなければ購入できない。政府が政策を実行しようとしても、国庫がなければできない。それを供給しているのは唯一、中銀である。したがって、中銀の信用創造なしには、金融システムをスタートできない。では中銀の「融資」に対応する貸付債権は何か? 中銀に口座を持つのは政府と銀行だけだから、彼らへの貸付債権が発生していることになる。そして国債とは単にこのときの政府貸付債権が形を変えたものにすぎない。これによって獲得した国庫や準備預金を元手に、政府の財政政策や銀行融資が行われていく。 つまり、政府の債務とは、その経済圏において政府から発行されたベースマネー総額のことに他ならない。
政府の債務は、そもそも中銀システムそのものを運用するにあたって必要不可欠である。これらを償還するということは、実質的に現在の貨幣経済を停止させることを意味する。
プランク定数は"いつ"必要?
プランク定数は”量子論の”物理定数なのか?
量子力学を特徴づける物理定数としてプランク定数がある。
プランク定数は前期量子論、いわゆるヒルベルト空間だの作用素だの測定理論だの言い出すずっと前から登場していて、例えば量子化された光のエネルギー1単位として登場する。
他にもド・ブロイ波長
また、そこから派生して運動量演算子
さらにはシュレディンガー方程式にも登場する。
プランク定数は作用の次元を持つ。つまり、運動量×距離、またはエネルギー×時間だ。
これほどまでに量子論/量子力学の随所に導入されているにもかかわらず、プランク定数の解釈には釈然としない点があると思う。
例えば、「極限が、古典理論になる」というスローガンがある。これは
といった性質によって支持されている。
しかし、どうだろうか? 率直に言えば、僕はこの説明、嫌いである。
例えば、不確定性関係や、それを備えた作用素確率論としての構造は、単に形式的ににしたからと言って消えるものではないはずだ。そもそも、古典力学と量子力学では、数学的構造があまりに違いすぎ、パラメータの極限等といったちゃちな解釈でその対応を正当化できる代物ではない。そもそも、
は定数なので、動かしようがない。第一、掛け算作用素と微分作用素が、プランク定数をゼロにしたからといって可換になるわけがないではないか。
しかしこうした議論はもとから非形式なもので、まともに取り合うべきではないとしても、もっと根本的な違和感がある。より現代的な量子力学の教科書、測定理論や量子計算を想定した文献では、そもそも最初に前期量子論的議論を行わないこともあり、プランク定数が登場するよりもはやく具体的な系を議論出来たりする。まずで議論し、スピンは無次元のパウリ行列を使えば良い。こうした場合にプランク定数が出現するのは、シュレディンガー方程式の時間微分項の隣であり、その登場は唐突ですらある。
そもそも(質点粒子系に限らない)シュレディンガー方程式の主張は、実質的にはストーンの定理そのものである。つまり、1パラメータユニタリ発展は、自己共役な生成子を持つという主張に過ぎない。そうであれば、プランク定数を導入する理由とは一体なんだろうか? あるいはハミルトニアンをエネルギーの次元にする理由は? そしてその係数が非常に小さくいながら、あまりに「具体的な」値にしなければいけない理由はなんだろうか?
現代的な量子力学の定式化は、少なくとも定式化のみに限れば、プランク定数をそもそも必要としていない。そうなればもはや「プランク定数は量子論的スケールを特徴づける」とは言えなくなる。
しかしながら、依然としてより「具体的な」系のモデルを議論するにあたって、プランク定数は絶対に登場する。プランク定数は一体いつ必要になり、その解釈は何なのか?
物理量を生み出す変換群
僕は量子力学における正準量子化をずっとしぶとく嫌っているのだが、嫌うだけでは建設的ではない。そこで代わりになるものとして、群作用、高級な言い方をすれば調和解析がその(本来の)代わりだと思っている。
例えば正準量子化が「成功する」とされるいくつかの物理量、グローバルな位置演算子、運動量、自由なエネルギー、場の演算子などは、実際には正準量子化はほとんど必然性が関係がない。
位置演算子は、ヒルベルト空間を、そのグローバル座標の空間に取った段階で先験的に与えられるし、運動量は対称性変換群の生成子であり、エネルギーはそのカシミール元、場の演算子は、負周波数空間の双対修正と第二量子化(Fock)関手を経たラダーオペレータそのものだ。つまり正準量子化の背後には、(全てではないものの)よりもっともらしい、それぞれのロジックがある。
そのうち群作用はもっとも重要なものだと思う。量子力学と古典(解析)力学はあまりにも構造もその解釈も違いすぎる。しかし、古典量子どちらも
- 群作用ができ
- それによって変換の生成子を誘導でき
- さらにそれらのリー代数を住まわせる空間を備え
- 生成子を物理量(共役運動量)と解釈でき
- 対称性が満たされる場合はにはそれが保存する
ところまで共通しているのだ。だから、正準量子化のような、「古典系を参考にする」ということが成功するのだとしたら、その理由は正準交換関係ではなく、共通の群作用によってである。
最後の、対称性が満たされる場合に、共役運動量が保存する、という性質は、よく考えるに値する。例えば、作用反作用を満たす2物体が相互作用しても運動量が保たれるように、対称性を満たす2系の合成系においては、それらの運動量はあくまで全体量が保たれていればよい。
これは 2系が全く異質であっても言える。 群が作用する系
が、全く異質な系であっても全体系のハミルトニアンが
対称であれば、
上の共役運動量と、
上の共役運動量の総和は保存する。しかし、
上の共役運動量は、単独では保存しない。
これは当たり前のことを言っているのだが、それは「運動量」というものに我々がよく親しんでいるからである。全く異なる系同士の、適当な物理量を、なぜわざわざ足そうとしたのか、そして、なぜそれが保存的に交換すると思ったのか。 それは、この2つの系に共通の群が作用していたから だ。
この意味で群作用は、異なる合成系同士の物理量を「足す意味がある程度には同種のものである」と見なす動機を与える。
量子古典を同時に考える
そこで話をプランク定数に戻すのだが、同じ群が作用している異なる2つの力学系を議論するにあたって、古典⊗古典や、量子⊗量子はよく議論されるものの、古典⊗量子、という系を議論することは見かけない。もしあったら教えてほしいのだが、ここにプランク定数が登場する必然性があるのではないか、という説を思いついた。
古典系と量子系にともにが作用している。これらはそれぞれシンプレクティック変換、およびユニタリ変換として作用しているとしよう。そうしたときには、
のリー代数の元
ごとに、
だとか
だとかなる関数や自己共役作用素
があって、
は先の群作用の軌道を再現する、ということになる。
ところで、同じに対する生成子なのだから、前節の直感からすると、この2つの物理量を足す動機が出てくる。 片方は相空間上の関数、片方は自己共役作用素だが、同じ対称性変換群から来たものなのだから、足せるはずだし、もし「全体系ハミルトニアン」(ハイブリッド系のそれがどのように表現されるのかはまったく想像もつかないが!)があって、それが
不変なら、この全
運動量は保存的に 交換する ことすらできるはずである(いったいどうやって!?)。
どうやってそれを実現するのか、これはわからない、とにかくハイブリッド系のダイナミクスを表現する数学的道具が発達するのを待つしか無いが、ともかく、と
を足す動機がある ということはわかる。
しかしここで問題が発生する。量子系のユニタリ変換は、生成子をパラメータで指数写像するだけだから、の次元は、
パラメータの次元の逆数である。しかし、古典力学はそうではない。ポアソン括弧は
による微分が入っていて、それを相殺するように、
は作用の次元と
の逆数次元の両方を持っている。
これによって、「同じ群作用の共役運動量なのにそれを足すことができない」 という問題が発生する。
作用の次元
どうしてこんなことになるのか? よく考えてみれば、解析力学において、ハミルトニアンやラグランジアンはエネルギーの次元をもっていて、その積分である作用も当然有次元量だった。やポアソン括弧の次元も全てここから来るものである。
しかし待ってほしい、ラグランジュ形式にせよ、ハミルトン形式にせよ、その定式化は最小作用であり、その絶対的な値には物理的意味がない。作用は最小化されることが本質だから、その次元がどうとか、値がどうとかは「物理に効いてこない」のだ。 にもかかわらず、我々はそれを相対化したり、無次元化したりなどしなかった。それは、解析力学以前の古典力学との接続を保つためだったりするのだろうが、とにかく相対化を怠ってきたのだ。
さて、今こそそれを相対化しよう。それによれは、適当な 作用の次元を持つ任意の定数 を使って、これで割ったものを、本当のラグランジアンだとかハミルトニアンだとか言うことにしよう。
するとどうなるだろうか? 運動量の次元は位置の逆数になって、ポアソン括弧は無次元化するのである。先のと
については、それが住んでいる数学的世界はわからないが、ともかく
のようなものを作ることは、少なくとも次元解析はそれを妨げなくなる。は、この謎のハイブリッド系の合成を意味するが、とにかくわからないので
と記した。将来の数学に期待。
しかし、一体の具体的な値は何にすればいいだろうか?
の次元を決めはしたが、その値は決めていない。
ここで一つ、祈りを捧げる。
この謎ハイブリッド系を、とりあえずそこそこに孤立させ、による対称性が成り立つ状況に置く。そしてそれを守る限りで相互作用をさせて、
を測るのである。
には
が含まれているので、
を決定するには
を決めないと行けない。ところが、このような実験をしているときに、我々はあることに気づく。
を特定の値にとって、実験結果を集計すると、
が常に実験の前後で保存しているのだ。
そこで、我々はをその値に固定して、これを恭しくプランク定数と名付ける。
ここで捧げた 祈り とは、要するに 「量子古典のハイブリッド系でも全体運動量に対するネーター定理が成り立っていてくれ」 というものだ。これは祈るに値する。なぜならこれによって量子系の物理量に、古典系の物理量
を媒介した物理的解釈を与えられるからである。
以上が先日思いついた、もし前期量子論や歴史的経緯を完全に無視してプランク定数を動機づけるとしたら、このような形になるのではないか、という一つの仮説だ。
つまるところ、要点は以下である。
ハイゼンベルク描像と時間発展
ハイゼンベルク描像
量子力学をシュッとやると、ハイゼンベルグ描像というのが登場します。
通常扱われているシュレディンガー描像というのは、要するに状態が時間発展します。一方でハイゼンベルク描像というのは、事象や物理量の側が時間発展します。
非常に素朴な理解 では、量子力学が計算するものは、ある状態()における、ある事象や物理量演算子(
とする)の期待値
であるとされます。そこで、シュレディンガー描像において、ユニタリによって、状態が
と発展しており、事象や物理量がそのままであるなら、代わりに事象や物理量が
と発展し、状態をそのままにしたとしても、変化後の期待値はどちらも
なので同じである、というのがそのざっくりとした説明です。ついでにこの間の子である相互作用描像というのもあり、摂動展開などで使われます。
これだけ見ると、「ふーん」以上の感想はありません。
現代的なYet Anotherハイゼンベルク描像
さて、ここで対比として持ち出したい、「もう一つの」ハイゼンベルク描像があります。
量子測定や量子計算の理論はじわじわと普及しつつあり(要出典/希望的観測)、すでにユニタリ作用素はすでに一般的な量子プロセスと呼べるものではなくなっています。
かなり一般的な量子系の発展プロセスとして、CPTP写像というのがあります。 これは、
と定義されます。これが真に最大限一般的なものか、というのは微妙な問題ですが、相当に一般的なものとして受け入れられていると思われます。トレース保存は、確率の正規化を保つことであり、完全正値は、この写像が記述していない外部の量子系があったとしても、正値性という基本的な性質が損なわれないことを要求します。
完全正値がやや人工的な条件に見えるために、これを落とした場合にどういう事が起きるかについては、
https://www.sciencedirect.com/science/article/abs/pii/S0375960105005748
などで議論されています。(昔読めたが今はアクセス権を喪失してしまった...)
しかしここでは完全正値の動機づけは本質的な話題ではないのでスルーします。
CPTPは次のように展開できることが知られ、これはKraus演算子と呼ばれています。
CPTPは量子状態の変換なので、シュレディンガー描像に対応するものと思えるでしょう。CPTPはトレースクラス間の写像となっていますが、量子状態は特に密度行列で書かれることを考えると、より適切な"型"は、を
上の密度行列として、
と書くべきです。
ところで、これに対する双対があります。量子状態が密度行列で表現される一方で、
量子系の事象は、Effect作用素で表現されます。密度行列が、トレースクラスでトレース1規格化されたものであったのに対し、Effect作用素は、以上
以下の有界作用素です。
これについての話を展開する前に、一般確率論における双対性を述べておきます。
密度行列とEffect作用素を、状態だの事象だの言うときには、背後に次の(一種の)一般確率論的な枠組みを意識しています。すなわち、
- 状態
は、凸空間である。(
]について、
の"内分"演算ができる)なぜならば、
- 状態は確率混合可能である
- 事象
は、Effect Moduleである。なぜならば、
- 排他的事象は(頻度的に)合算可能である
]のレートで事象をロスできる
- 状態と事象に対して、その発生確率がある。つまり、
]がある。これは、
について凸準同型であり、
についてEffectModule準同型である
EffectModuleはEffectAlgebraの ]moduleであり、筆者がこれを知ったときには、その定式化の素直さの割に、界隈にあまり普及していなかった感がありますが、今はどうなんでしょうね。
量子力学は、、
、
による、一般確率論の一種と思えます。
そして、ある種の 位相的に都合のよい 一般確率論(量子論を含む)では、次の双対性が成り立ちます。
すなわち、状態空間上の凸写像はすべて事象であり、事象空間上のEffctModule準同型はすべて状態です。量子力学におけるこれは、関数解析の事実としてよく知られており、
つまり、
ということです。
この双対性が成り立っているような一般確率系では、シュレディンガー描像/ハイゼンベルグ描像のような、2つの等価な世界で系を記述することができます。
ひとまずは量子系で議論をしましょう。CPTPは一般的な状態発展でした。ところで、量子系においては上のような双対性が成り立ちます。そこで、CPTP写像を使って、
という写像を作ります。双対性から、あるがあって、
となります。(このあたりはRieszの表現定理とほとんど同じことをしている)
ここで、という写像を考えることができます。これを
としましょう。これは、Effect作用素をEffect作用素に移す、EffectModule準同型です。つまり、事象の空間の"発展"写像です。
この構成は、が別に完全正でなくてもできますが、完全正であれば、
も同様の完全正性を引き継ぎます。
のトレース保存性は、ここでは
の保存性として継承されます。
このタイプの写像の標準的な名前があったかどうか忘れてしまいましたが、ひとまずCPU写像と呼ぶことにしましょう。つまり、Completely Positive Unitalということです。
このCPU写像が、相当に一般的な、量子的事象の発展写像であることも、CPTPと同様です。つまり、という最も自明な事象(常に成り立つ)を保存し、かつ事象(Effect作用素)を事象に移し、その正値性は、完全である。
CPU写像から、CPTP写像を作ることも全く同様にできます。
CPU写像を使って、
という写像を作ります。双対性から、あるがあって、
CPU写像は、Effect作用素、つまり事象を変換する一般的な写像ですが、事象のCPU写像による量子論と、状態のCPTP写像による量子論は、 と Gleason/Buschの定理によって、完全に等価です。それは
によって、圏同値なので、どちらで扱ってもよいことになります。
、
は、この圏同値による対応にほかなりません。
CPUもCPTPも、非常に一般的なクラスの写像です。ユニタリはもちろん、例えば、系の自由度を拡大したり、相関をもたせて片方を削除して乗り換えたり、新しく系を増設して相関させたり、確率混合したりなど、極めて幅広い操作ができます。それらの操作は状態側で行っても事象側で行ってもよく、圏同値がその整合性を保証します。
CPTP写像が状態を変換する一方で、CPU写像は事象を変換するので、後者はハイゼンベルグ描像に対応すると言えます。
.
.
.
.
.
.
.
.
本当でしょうか?
何かおかしいぞ
前節で現代的な量子論におけるプロセスの話を展開したときに、CPU写像の型のメタ変数を、CPTP写像の型のメタ変数と逆にしていたことに気づいたでしょうか。
これは、仕様 です。そもそも、一般確率論的にも、状態と事象は、確率関数によって反転するようにできており、その圏同値は、反変です。は 反変関手だからです。
これは何を意味するのか。例えば、によって、状態を発展させる、というとき、この発展が時間順方向であるとしましょう。そのとき、これの事象側の対応物
は、時間逆方向です。
は、未来に測定する可能性のある事象を、現在に持ってくる写像なのです。
さて、ここで最初の話に戻ってくるのですが、最初に述べた、Yet Anotherではない、教科書でよく登場するハイゼンベルク描像は、なんと時間順方向です。 ということは、なんとなくYet Another ハイゼンベルク描像とか名付けてみたけど、普通に別物です。一般化になっていません。
つまり、現在2種類のハイゼンベルク描像があるのです。なんということだ。
ちょっとまてよ、じゃあ一体ハイゼンベルク描像ってなんなんだ? というのも、Yet Another ハイゼンベルク描像は一般確率論的な動機づけから出てくるものであり、その操作的解釈はあまりに自然です。逆にこれまでのハイゼンベルク描像は一体何をしていたのか ?状態ではなく、事象を発展させる、というアイデアから、なんでまったく逆方向の写像がでてくるのか?
ハイゼンベルク描像が本当にやっていること
Yet Another ハイゼンベルク描像で、Riesz双対っぽい構成をした時のそれと、 通常のハイゼンベルク描像での整合性要件は、全く同じ形をしています。
にも関わらず、その解釈は全く逆です。
- 前者は
を時間発展だと主張し
- 後者は
を時間逆発展だと主張します。
そんなことってあるんでしょうか?
さてここで、筆者の見解を述べておきます。異論は認めるが認めないかもしれない(えっ)
時間発展解釈を捨てるべきは、古いハイゼンベルク描像です。
かつてのハイゼンベルク描像がしていたことは 時間に依存するゲージ変換 です。
このことを把握するために、視点の回転が要ります。素朴な量子力学では、時間発展とは、あるヒルベルト空間(のトレースクラス作用素の空間)を、ベクトル(か密度行列)が動き回る、というイメージで把握するかもしれません。少なくとも古典力学はそのような形をとります。つまり、時間軸という数直線から、状態空間への写像があり、これをたどることが状態発展だという見方です。
しかし、より一般的なプロセスでは、そもそも異なる時間で同一のヒルベルト空間に収まっている保証はありません。
さらに、この見方はあまりに状態と発展が密結合した見方です。発展は、あくまで状態空間全体への操作です。その作用の結果、発展パスを書けることはありますが、発展の本質はあくまで状態空間から状態空間への写像です。古典力学だって、運動の本質は、相空間の自己微分同型のことです。
そうした場合を含む場合、時間軸に状態空間の要素を割り当てる前に、まず状態空間そのものを割り当てる必要があります。

これはちょうど、時間軸上に、状態空間そのものをファイバーとして載っているバンドルを考えるようなものです。ただし、一般に全てのファイバーが同型だとは限らない点は違います。
そして、ことなる時間の間に、状態空間の発展写像が入ります。これはCPTPです。ユニタリとは限りません。
事象の側も同様に捉えます。ただし、事象の写像はCPUで、これは状態側とは向きが逆になります。

さて、それでは、ハイゼンベルク描像とは一体なんだったのか?
ここで思い出すべきは、量子力学の内容は、基本的にユニタリ同型の範囲で変わらないということです。つまり、事象も状態も全てユニタリ変換するのならば、その変換は相殺されて表に出てこないということです。
この、ユニタリゲージ変換とでも言うべき操作を、各時刻で別々に行う ことを考えます。つまり、という時間
に依存するユニタリ変換を考えて、時刻
の状態
を
へ、同様に時刻
の事象
を
へ写像することを考えます。全体のユニタリ変換なので、状態も事象もまったく同じ変換になっていることに注意してください。

このとき、
- 時刻
の状態
を、
- 新しいゲージで
- 写像によって時刻
に移したもの
と
- 時刻
の事象
の
- 新しいゲージでの値
で評価をしたいとします。それは
という形になります。
さて、ここで 偶然、まったくの偶然 ですが、
が成り立っていたとしましょう。すると
となり、先と全く同じ式が得られます。
つまり、ハイゼンベルク描像とは、事象の時間発展ではなく、 時間発展に相当する操作や写像は別途存在する上で、 時間に依存するユニタリゲージ変換の一種で、それが状態の時間発展を相殺する場合なのです。
ハイゼンベルク描像と、一般確率論の双対性で、時間の方向が逆になっているように見える謎がここでとけます。 という変換は、時間発展ではありません。 この変換の前後で、作用素は 常に時刻
の事象空間の中にあり、状態の時間発展を相殺するようなユニタリの、時刻
の変換がそれだったということです。
P.S.
(幾何厨としての)信仰告白
まず、関心のある系があります。

これは絶対的なものです。なにか知らないがとにかく"在り"ます。 しかしあるだけでは地上の民の我々にはまったくそれに触れることも知ることもできません。 我々は、いくつかの馴染みのある(数学的)構造を持っています。例えばユークリッド空間などですが、他にもあるでしょう。 そこで、天界におられる系に、我々の良く知っている構造に降りてきて頂きます。

この写像、天界からの使い、使徒たちを、成分表示だとか、自明化だとかいいます。 こうして我々は馴染みのある構造に天界の系の影を見出すことができます。 系はとても複雑ないし大きなものであられることがあり、こうしたことは、系全体でなく、一部について行われることもあります。 まことに天界の系は大きなお方であり、使徒達を通じたとしても、私達にはその姿を一望できるとはかぎりません(一望できることもあります)。

天界の系は、まことに精妙なことに、私達がそれに見出そうするさまざまな振る舞いを持っています。あるものは代数構造を持っています。あるものは、また他の系との派生関係や写像をもっています。自明化はそうした系の方々のお姿も私達に示してくださいます。このようにして、我々は天界の系のお姿を、地上の物事の振る舞いを通じて、さらによく知ることができます。


私達が天界のこうした振る舞い、代数構造、派生構造、関係について述べる時、私達は畏れ多くも、それを「定義する」と呼びます。
このようなこと我々がするのは、やはり我々が直接触れるものが、地上のものに限られるからです。
私達は天界の系の関係や性質をよりよく知るために、その模造物(👆のなど)を地上で作り上げる必要があるのです。
その模造物が天界の系をよく反映するように、上記のような可換性を要求します。これは準同型性だとか関手性だとか呼ばれているものです。
ここで、重大な真理があります。系のお姿を我々にお示しくださった自明化は、ただ一つのものではないことがあります。天界の系はただ一つの方ですが、それが我々の目に映る時は、一般にさまざまな姿をとられます。

彼らは私達に系のお姿を知る機会をもたらしますが、また、系のお姿を誤って見せうるものでもあります。私達は、こうした自明化たちに正しく向き合い、系のお姿を正しく捉える必要があります。自明化が私達に見せたユークリッド空間の影は、まさに影なのであって、影そのものをいかに凝視しても、系の真のお姿はそこにはありません。
幸いにも、自明化達は、ある構造をもっています。それは私達が群と呼んでいるもので、しかしそれ自体は群ではありません。自明化たちは、群が推移的に作用することができるものです。つまり、ある自明化を群の単位元に対応させた時、他の自明化がすべてその群の元として相対的に決まるようになっています。このような群を構造群だとか、ゲージ群だとかよび、ある場合には、自明化達のことを主束と呼びますが、ここでの考え方はゲージ理論に限ることではありません。このような見方は至るところに見いだされ、実質、私達が天界に向き合うにあたって、このことから逃げることはほとんど不可能でしょう。

私達が天界の真理を知るためには、こうした自明化たちを振る舞いを取り除く必要があります。自明化たちを切り替えた時に、それが群で書かれる、ということは、つまるところ、私達が作っている天界の模造物には、群が作用するということにほかなりません。

しかしながら、この群作用は、私達が自明化の使徒達を介して天界を仰ぎ見るときの、単なる見方の違いに過ぎません。この群は、系それ自体には作用していません。
私達は、天界の振る舞いを知るために、天界が持っている構造や関係や派生構造について、それらの地上の模造物を「定義する」ことを試みます。

しかし、すでに見たように、自明化は、天界の姿を多様に変化させて、私達に見せようとします。私達は天界を仰ぎ見るにあたって、それらの変化を割り引く必要があります。つまり、自明化を相対化する必要があります。ここで、私達にできることの、2つの両端があります。
ひとつは、を、自明化に完全に依存させることです。今現在、天界のお姿を我々に示している自明化
がなんであるかを完全に把握した上で、それぞれの自明化ごとに、模造物の演算
を次を満たすように作るというものです。

これは確実に動作しますが、とても骨が折れる作業です。当初の自明化と異なる自明化に対して、いつでもそれを計算する用意が求められます。つまり、
に対して、すべての
を計算する必要があります。例えば、直交座標で定義したラプラシアンを、任意の座標系で計算しようとすることを考えてみましょう。
もう一つの問題点として、今現在参照している自明化が、本当になのか?ということを、私達が知ることが不可能だという点です。それはニュートン的絶対座標のようなもので、ある種のものは、事実不可能です。私達は、自明化の使徒の名前を知ることができず、ただかれらの階級とその群構造についてだけ知ることができます。
逆方向の極限は、最初から、ただ一つのを定義するということです。つまり、自明化に作用する表現
達にたいして、次が成り立つものだけを考えます。これは、まさしく天界がそのようなものを自然に備えているとき、しばし可能になります。これは自然変換だとか、intertwinerだとか呼ばれています。

このようなことができるとき、間違いなくそれは天界の秩序を示しています。しかし、こうしたものは一般には希少です。私達は畏れ多くも、地上の模造物から得た着想の、天界での対応物を知りたいと思うことがあるでしょう。しかしそうしたものが、この形で得られる保証はありません。
幸いにも、私達はこれらの折衷的なことができます。自明化の使徒たちに階級が存在し、その階級が構造群の部分群として現れることがあります。例えば、平坦な多様体の接束において、一般の座標系からくる成分表示はすべての自明化です。それらは可積分な局所GLを構造群にもちます。そのうちで、直線座標からなる部分を取ることができます。それらは大域的なGL(n)を構造群に持ちます。さらに、計量をつかって、直交座標からなる部分を取ることができます。それらは大域的なO(n)を構造群に持ちます。
すなわち、次のことをするのです。まず、自明化の階層を把握します。

そして、についてだけは、
をただひとつのものになるようにし、
それ以外の
については、
それ自体を使って定義します。

例えば、我々はユークリッド空間のラプラシアンを、任意の直交座標にたいして同一の定義で与えます。それは実際に一致します。しかしそれ以外の座標系については、泥臭い座標変換を実行します。
また例えば、ニュートン力学が、絶対座標系を知ることなく、ただ慣性系であれば、運用することができたのも、また、その運動法則が、慣性系においてのみ不変であるのも、こうした折衷によるものと言えます。つまり、ニュートン力学におけるとはガリレイ群だったということです。そこで、私達は様々な力や運動を、慣性系についてだけ定義すれば良くなったのです。慣性系においては、力は、0を原点として加法性が成り立ちました。非慣性系においては、慣性力が原点となるため、加法性が成り立たなくなりますが、そのことは計算によって確かめることができます。
以上が幾何厨の信仰告白です。要約すると以下のようになります。
- まず、天界に系があります。
- それを私達がユークリッド空間の要素であるかのように扱えるのは、ひとえに自明化の御業によるものです。
- しかし、自明化は一意的ではなく、また極めて多様に行うことができます。
- したがって、我々が、天界の何かを定めて操作するためには、その定義時に参照している自明化を固定するか、または、その定義が自明化に依存しないことを確認しなくてはなりません。
- 自明化が、その構造群に基づく階層構造を持っていれば、ある部分については自明化に依存しないようにさだめ、それ以外については、直接計算する、という折衷をとることができます。我々は直線座標や直交座標を都合よく採用することで、これを無自覚に行っています。
- この「自明化を相対化する」という作業は、 絶対に、絶対に、絶対に、避けることができません。すべての人が背負っている原罪です。
さて、この点を考慮に入れた上で、度々見られる次のような軸性ベクトルの導入が、幾何厨の信仰に著しく反したものであることを説明できます。
三次元ベクトル
の外積を、その成分について
としたとき、パリティ反転にたいして、外積の成分は変化しない。このようなものを軸性ベクトルとよぶ。
敬虔な幾何厨からみたとき、これが以下に間違っているかを述べましょう。
- 三次元ベクトルは天界におり、成分表示は、なんらかの自明化によるものである。
- ベクトルであるから、この自明化の構造群は
である。
- 外積を三次元ベクトルの、天界の演算として定めようとしている。
- この定義をある自明化について
であるとした。
- この定義は、
については、不変であるが、他では不変ではない。
- 自明化のパリティ反転を行ったならば、パリティ反転は
であるから、計算規則は不変ではない。
この議論の罪深いところは、不遜にも、地上での成分の計算規則を、天界の演算そのものだと誤認したことにあります。成分によって計算できるのは、天界に居られるベクトルの、地上での模造物であり、それが天界の構造を反映していることを保証するためには、自明化を相対化しなくてはならない。しかしこの者は、という計算規則が立脚している自明化を相対化することなく、その不変性が保たれないような自明化の入れ替えを行い、それについて誤った解釈をしました。このものが見た軸性ベクトルとは、自明化の使徒が見せた亡霊にすぎず、天界にはそのようなものはないのです。
MMTに入門した
話題の理論に入門してみました。当方経済専攻でもなく、特に深い動機があったわけでもないし、政治的なあれこれの関心があったわけでもないです。
というよりは、僕はとにかく人間や社会における政治性がとにかく嫌いで、可能な限りそうした政治性や歴史性が脱色された機構的おもちゃが好きなのです。歯車とか。ピストンとか。経済の知見を得るとしたらなるべくそういう形の知識がほしい。物語性は敵であり総合性も敵です(えっ)。
そういう気持ちもあり、流行り物は好きではないのですが、流行り物だから拒否するというのもそれは不毛な逆張りだし、政策パッケージとしてのMMTとしてではなく、貨幣理論としてのMMTなら多少なり楽しめて得るところがあるのではと思ったのでした。
で、結論からいうと、得るところはありました。👆の本はだいたい米国事情ベースなのでそのあたりはよくわからなかったのですが、 貨幣理論としてのMMTの、少なくとも原理的な面はとてもシンプルで、
主権不換貨幣の総量は政策上の自由に操作可能な変数であって制約や目標ではない
というか、コレ以外の点はごく常識的で、実質的にマクロ経済の財政上の境界条件だけを修正したもので、 理論上は異端でもなんでも無い気はします。その境界条件だけ取り上げるとまた怪しく見えてしまうのですが...
というわけで、以下感想がてらに素人なりの理解を記しておきます。
貨幣価値 is 何
正直なところ、本当に内容は先の一行で説明が終わってしまっているのですが、 もうすこし踏み込むと、MMTは次のことを説明するように見えます。
貨幣とは何でその価値は何で担保されているのか?
通常、商取引で貨幣を支払うということは、取引商品とその貨幣が価格的に見合っているからこそ行われるのだと考えられます(その"価値"とは何で、どう測るかという問題はありますが、とりあえず取引主体が「交換してもいいかな」と思うことだとします)。すると、貨幣にはなんらかの価値があることになりますが、それはなにか?
AがBから財Xをn円で購入するとき、少なくともAのn円の価値はX以下に、またBはn円の価値をX以上に見積もっていないと成立しません。価値観の相違を許したとしても、少なくともBは貨幣価値を理解していないといけないことになります。つまり、Bはn円になんらかの価値を見出しているわけですが、それはなにかということです。
ここで話がめんどくさくなるのが、貨幣の通用性で、例えばAは、貨幣はBにとって価値があるなら、Bの財を引き出すためのトークンとしてAにとっても貨幣の価値がつきます。同様に、貨幣がCにとって価値があるなら、Cの財を引き出すためのトークンとしてBにとっても貨幣の価値がつきます。
つまり、「自分以外の誰かにとって価値がある」という性質はそれ自体が貨幣の価値の"可能性"の分枝に含まれるわけです。これはなんか、集合の帰納的定義みたいなやつで、通用性は貨幣の実効的な有用性の幅を広げるわけです。通用性が広がると、たとえばn円の貨幣は何時でも財Xと交換できるので、n円のほうが嵩張らないのでn円で持っておくか、ということができるようになります。つまり、その貨幣をユニバーサルな貯蓄として使うことができるようになります。
じゃあ、そうした再帰的な有用性の波及"だけ"で、貨幣が貨幣として機能するだろうか?と考えると、これは微妙な話になってきます。というのも、そういう意味の価値だけでいいなら、これは完全に流通コミュニティの価値観の安定性の話になってしまい、また実際そうして成立するトークンは存在して、暗号通貨とかはある意味そういう例に見えます。あれは一切の兌換性ももたず、アルゴリズム的に示量性が保証されていて、限定的ではあるのもの市場が存在します。ただし、ドルや円だとかの法定貨幣にくらべて、ビットコインのボラティリティ(変動の大きさ)は数十倍から数百倍あるわけで、資産や貯蓄として使うには非常に不安定です。さらに、通用性も非常に小さいです。暗号通貨を直接受け取ってくれる小売店は、法定通貨のそれとは比べ物にならないくらい少ないです。これはまさしく貨幣価値の担保がない事を反映しているように見えます。何の使いみちもないレアメタルを取引しているのと同じです。金のほうがまだ工業的使いみちがある分なんぼかマシかも。
租税貨幣論による担保
そう、法定貨幣、これが違いなのです。貨幣価値を担保するには、それに何らかの財なり権利が付与されているとするのが一番明快ですが、MMTはここで租税貨幣論をとります。つまり租税支払いに使える唯一のトークンなので、貨幣には価値がある(このことが法で定められているので法定)。何らかの政体の及ぶ地域に在住していれば、なんらかの租税が課されます。その支払いを怠ると、最終的にはなんらかの権利が剥奪されます。つまり、徴税状態は人権の次くらいに根源的な負の価値があり、それを解消できる(しかも貯蓄しておけば将来にあたってずっとそれができる)トークンである法定貨幣は正の価値があります。
ということで、貨幣それ自体には、租税支払いトークンという価値担保があることになります。
この租税支払いトークンとしての貨幣は、同時に債務証書としてみなすこともできます。つまり、権利証書のことですが、例えば借金手形は、「私phykmは何時までに何円返します」という証券のことで、それは言い換えれば「この券の所有者は何時以降phykmから何円もらえる」という権利であり、それがこの紙切れの価値を担保しているわけです。
一般に債務証書は、場合によっては不渡りを起こしえます。債務不履行というやつで、こうなった場合は、証券価値は消しとんでしまいます。通常はそうした証券の市場取引価格に、その分のリスクプレミアムが上乗せされるわけです。
では、貨幣を債務証書だとみなすとき、その内容はなんでしょうか? そうした契約書が存在するわけではないですが、法定貨幣故に、実質的には租税支払いを二通りで言い換えたものになり、
- 債権として: この券の所有者は、本券を債務者政府に手渡すと、租税義務のうち額面分を減免される
- 債務として: 債務者政府は、本券を受け取ることで、所有者に政府が課した課税義務のうち、額面分を減免する
ということになるわけです。すると、この場合、法定貨幣の「債務不履行」というのがどういうことか理解できます。つまり、
- 法定貨幣の債務不履行:租税支払いを指示通りに法定貨幣で完了したにもかかわらず、脱税とみなされて捕まる
という状態がそれです。まともに税制を運用している国家であればありえない状態であることが理解できます。
また、直接債務不履行を起こさなくても、貨幣価値の可能性が消滅するという状況がどんな場合かを考えることができます。(ここでは一旦為替:異なる貨幣間の相対価値のことは考えないとします)。つまり、租税による貨幣価値担保が消失することで、
- 完全な無税状態になる、または税制が設定されているが、強制力がなく、脱税が極めて容易である
という状態になります。これもまともに税制を運用している国家であればありえない状態であることが理解できます。 (もちろん、税制が消滅しても、それは貨幣価値の担保の可能性の一つが消えるだけなので、通用性のみによる価値は残ります)
税制が消滅とまでいかなくても、例えば減税や増税を行ったときにどうなるか、ということを考える事もできます。租税回避は、消費主体の選好のなかでもかなり強い傾斜がかかっているだろうことは予想できます。なにせ権利が奪われるので。
となると、消費主体の予算が一定であれば、税を重くすると、それだけ租税回避(支払い)に所得が食われ、それ以外の消費行動に割り当てる貨幣が減ります。すると、他の財を消費できなくなるので、需要が下がり、取引価格は落ちます。つまり、デフレ圧となります。逆に税を軽くすると、事実上可処分所得が増えるので、この逆が起きるわけです。ちなみに増税した場合、物価(実物財あたりの貨幣量)は下がりますが、同時に貨幣価値(単位あたりの貨幣そのものの価値)も下がっています。なぜなら、「税を回避する」という固定価値を獲得するのに必要な貨幣が増えているからです。
このあたりは市民的直観にも敵ってますね。なお本国はデフレなんだから減税しろという声も虚しく0->3->5->8->10と増税の一途をたどっています。
無限に刷れる理由
さて、貨幣価値が担保されたので、政府は安心して貨幣を刷ることができます。
何故か? 貨幣価値を担保している政府の債務とは、ゼロ円以上の税制を敷かれている前提で、 「発行貨幣による租税支払いを受領する」ことでした。 これは無限に履行できます。つまり、 無限に「借金(債務証書の発行)」をして、その「履行(租税支払いを受け取る)」ができます。 具体的には、支払ったその人を支払い済みリストに追加し、受けとった貨幣をその場で破り捨てるだけです。履行済み債務証書なので。
このあたりは「税は支出のための財源」という考えが間違っていることも示しています。すなわち、 貨幣価値の担保は「政府への租税支払い券」なので、それを履行した段階で貨幣は本来消滅するはずです。 政府の会計で、租税収入を支出に回す、というのは、履行済み債務証書を印紙代がもったいないからと言って再び使うようなものです。普通に考えれば支出にあたってすべて新規発行すればよいのです。一部twitterのMMTerの方々が、「税収とはお金を潰すこと」みたいなことを言っていますが、これは債権証書として考えれば文字通りの意味です。
おそらくMMTの反直感的な点は、貨幣という、日常的には当たり前に価値のあるものが、無限に刷れるわけがない、という気持ちだと思います。しかし、ここで見たように、実際には貨幣を債務証書とみなすことができ、さらに政府はちゃんとこの債務を履行しているわけです。そしてその履行の総量には物理的制約がない。これが無限に刷れることの理由です。(逆に言えば国家消滅の危機みたいな、税がなんぼのもんじゃいみたいな事態になれば、貨幣価値担保も怪しくなる)
貨幣以外にも、自国通貨立て国債も任意の額発行できます。これも不履行になりえません。あえて政府が償還を拒否すれば起こせますが、そんな馬鹿なこと(ちょっと見てみたくはある...)をするくらいなら貨幣を刷るか、借り換えるでしょう。自国通貨なので満期償還時に必要なだけ刷ればよいからです。というか、国債というのは、実質的には時限と利子がついた貨幣のことです。利子以外の部分は、「印刷したこれは貨幣だったのか否か」の判断を満期償還時まで遅らせることができる貨幣です。
ということで、
- 主権(発行権と徴税権をその政府が持っている)
- 不換(他の財や他国貨幣との兌換性を政府が保証しなくてよい)
な貨幣は、 その政府にとって、制御可能な変数です。制御可能とは、 政策によって自由にその総量を調整できるということです。 例えば増税するか、支出を絞れば、貨幣総量を減らせます。逆に減税する(恒久的無税にまではしない)か、貨幣を刷って支出すれば、貨幣総量を増やせます。貨幣総量を増やすことを財政赤字と呼び、貨幣総量を減らすことを財政黒字というわけです。
そして貨幣は、こうした任意の制御が可能な"唯一の"財です。
つまり、貨幣は自由に操れるが、それ以外の実物財が操れる保証はないのです。
このことはケルトン本でも何度も強調される重要な点ですが、 政府は国民によい生活なり環境なりを提供するために色々やるわけですが、 例えば、うまい飯を食わそうとしても、農地と農業従事者が無ければどうしようもなく、 ハイテク機器でIoT!などとのたまっても、ハイテク産業の工場と技術者が無ければどうしようもない。 情報人材!介護人材!と叫んだところで、教育された人材、または教育インフラが整ってなければ、出てきようがありません。 かと言って、当然政府がそれを持っているわけでもありません。 したがって、これらは間違いなく示量的な財に関するビジョンですが、政府はこれを直接操作できる保証がありません。
しかし、主権をもつ貨幣だけは制御できます。税制を変更し、貨幣を印刷するか、租税支払いを受領すればよい。 そして、少なくとも国内に関しては、その貨幣の需要は租税の存在で担保されているため、 国内市場にある財に関しては、刷った円でそれを購入できます。もちろん政府が消費するわけではないので、 それを然るべき必要な場所に変換して配置します。つまり実質的には支出というのは国内の財の再割当てのことです。
つまり、もし政府が財Xが沢山欲しいという場合、国内調達する手段としては、
- Xの生産部門に支出(投資)して生産力を上げてもらう
- 生産力が上がるのを待つ
- Xを購入する
財Xがもういらないとあれば、
- Xの購入をやめる
- 必要に応じて労働者の再就職を支援する
みたいな手続きを踏む必要があるわけです。つまり、 貨幣をどのタイミングどこに割当て、どこから取り、その結果実物経済に何が起きるかだけが問題であり、 その収支は問題にはならないことになります。
ということでケルトンは著書のなかで「本当の制約は実物財の方だ」という旨のことを何度も強調しているわけです。
貿易を考えると、もう少し政府が打てる手段は変わりますが、主権不換貨幣の総量をコントロールすることについて制約が無いことは同じです。自国通貨換算で貿易赤字(相手国が自国貨幣保有を増やしている)であっても、だからどうということにはなりません。むしろ自国の公的決裁にしか使えないトークンをもらって実物財をよこしてくれているのでありがたい話とも言えます(とはいえ輸入目的で無限に刷れば自国通貨安になって輸入が持たなくなるため、それは考える必要がある。相手国にとって、この貨幣の価値は自国経済の財を購入できるという点なので、例えば貨幣を刷って輸入すると同時に、自国産業にも投資して強化する等)。
つまり、財政の主要な課題というのは、政府が赤字かどうか(支出と税収の差額)ではなく、
という点(のみ)です。もしここに望ましくない効果が予想されるなら、それは調整する必要があります。よくMMT批判として出てくるインフレ懸念もこの一部です。例えば、民間需要がある財Xを政府が(例えば輸出のために)買い占めたりすれば、供給が不足して価格が上がります。またありえない話ですが、支出において一切財を購入することなく、一人当たり1億円を配るみたいなことをすれば、それだけ価格も上がるでしょう。こんな馬鹿げた額を唱える人はいませんが、これが10万とかであれば、現にこの間の特別給付で実施され、結果として大した問題もなかったということになります。
不換貨幣の発明
こうしてみると、主権不換貨幣というのはものすごい発明に思えます。
まず不換性ですが、以前は幾つかの通貨は金と貨幣の兌換性があったわけですが、これはどういうことかというと、政府が金と貨幣のコンバーターとして振る舞う必要があるわけです。これが市場に任されていれば、価格変動によってどこかで均衡するはずですが、兌換性を保証してしまうと、 「物理的に異なる2つの財のコンバーター」という、そのものからして物理法則に反する機能を政府や銀行が押し付けられてしまうのです。 物理学のアナロジーを考えれば、これは無理筋だと想像できます。例えば「1リットルあたり1ジュールで交換します」みたいな機械が破綻をきたすのはほとんど明らかでしょう。だから、物理法則がその互換性を保証していないような財に対して、兌換としてはいけなかったのです。あるいは、その総量を常に把握して管理する必要がある。
それから主権ですが、貨幣を刷っても、それに需要がなければ広く使われることはないわけです。兌換性はそのわかりやすい担保でしたが、物理的に無理がありました。また通用性と示量性だけでは暗号通貨のように限定的にしかならないし、価値も不安定になります。そこで、租税に関連付けることで、行政の届く範囲において広く普遍的な需要を喚起でき、決裁・貯蓄手段として普及させることができます。この貨幣の債務は税の受領という抽象的な行為で行われるため、履行は無制限にできます。つまり、政府が発行することについて特に制限はない。物理学のアナロジーで言えば、全ての熱力学系に、貨幣という新しい示量変数を追加するようなものです。政府はこの貨幣の熱欲を持っています。 不換なので別の財との交換を政府が求められることもなく、それは市場が勝手にやります。 常に偽造を取り締まるというコストは掛かりますが、貨幣自体の物理的価値がほぼないことと合わせて、政府は貨幣総量を自由にコントロールできるようになります。
そうすると、どうやってこのシステムが成立したのか?という疑問も出てきます。また、主権不換通貨がよくできたシステムなら、とっととそうでない国もそれに移行すればよいのではないか?
これは歴史的経緯や国際関係が効いてくるはずで一概には言えないでしょうが、例えば国内産業に乏しく、生活必需品の大半を輸入に頼っているような国の場合、そもそも独自通貨を発行しても、支出先が無い(受け取ってくれる自国産業がない)ということはありえる気がします。すでに生活の大半が外貨で回っている場合に、新規貨幣に乗り換えさせるに十分な需要を喚起するには、租税を用いても難しいかもしれません。その意味ではいま現在このシステムを存続させている国はある意味幸運かもしれません。
Fock空間 via StringDiagramで完全理解する確率過程:Revisited portal
以前
を書いたのですが、実はこの議論の背後にStringDiagramによる極めて雑な計算が隠れており、それを端折った故に、謎の数式が書かれただけの怪文書になってしまっています。
あれから色々続編を考えおり、その結果として、割と話が膨らんで面白くなってきたんですが、しかし計算につかったString Diagramをタイプセットするのは異常につらく、かつ計算も雑なためにきちんと定式化/フォーマルな文書にまとめるモチベが低く、あれそれしているうちに半年が過ぎました...
しかしこのまま放置するのもどうなんという思いと、一抹の数物的寂しさを覚え、もう手書きでいいからダラダラと書いたものを公開してしまえ、という気分になったため、iPad使って計算を書き直して公開していくことにしました。
個人的な書きやすさから、本体をesaに書いており、記事をはてなに移そうかと思ったものの、tex記法が非互換などでハチャメチャに面倒なので、ここをポータルにします。書き次第追加していきます。esaにはコメントできるかわからないので、なにかありましたらtwitterかこの記事へオナシャス
パート1(Boson Fock via String Diagramと色々概念対応)
10/8 up
パート2(Gauss過程/Poisson過程/Levy過程とLevy Khinchine定理)
10/8 up
(予定)
パート3(Parthasarathyの伊藤積分と伊藤公式についてホニャララ)
パート5(確率過程を微分する)
パート6(なんか応用する)